Schatting van deelname aan SQL Server met behulp van grove uitlijning van histogram

De belangrijkste wijzigingen die zijn aangebracht in Cardinality Estimation vanaf de release van SQL Server 2014, worden beschreven in de Microsoft White Paper Optimizing Your Query Plans with the SQL Server 2014 Cardinality Estimator door Joe Sack, Yi Fang en Vassilis Papadimos.

Een van die wijzigingen betreft de schatting van simple joins met een enkel gelijkheids- of ongelijkheidspredikaat met behulp van statistische histogrammen. In de sectie met als titel "Join Estimate Algorithm Changes", introduceerde het artikel het concept van "grove uitlijning" met behulp van minimale en maximale histogramgrenzen:

Hoewel mogelijk minder consistent, kan de oude CE iets betere schattingen van de toestand van een enkelvoudige verbinding produceren vanwege de stapsgewijze uitlijning van het histogram. De nieuwe CE maakt gebruik van een grove uitlijning. Het verschil in schattingen kan echter klein genoeg zijn om minder waarschijnlijk een probleem met de kwaliteit van het plan te veroorzaken.

Als een van de technische recensenten van het artikel was ik van mening dat een beetje meer detail over deze wijziging nuttig zou zijn geweest, maar dat heeft de definitieve versie niet gehaald. Dit artikel voegt wat van dat detail toe.

Voorbeeld grove histogramuitlijning

De grove uitlijning voorbeeld in de White Paper gebruikt de Data Warehouse-versie van de AdventureWorks-voorbeelddatabase. Ondanks de naam is de database vrij klein; de back-up is slechts 22,3 MB en kan worden uitgebreid tot ongeveer 200 MB. Het kan worden gedownload via links op de AdventureWorks installatie- en configuratiedocumentatiepagina.

De zoekopdracht waarin we geïnteresseerd zijn, voegt zich bij de FactResellerSales en FactCurrencyRate tabellen.

SELECT
    FRS.ProductKey,
    FRS.OrderDateKey,
    FRS.DueDateKey,
    FRS.ShipDateKey,
    FCR.DateKey,
    FCR.AverageRate,
    FCR.EndOfDayRate,
    FCR.[Date]
FROM dbo.FactResellerSales AS FRS
JOIN dbo.FactCurrencyRate AS FCR
    ON FCR.CurrencyKey = FRS.CurrencyKey;

Dit is een eenvoudige equijoin op een enkele kolom dus het komt in aanmerking voor schatting van join-kardinaliteit en selectiviteit met behulp van grove uitlijning van histogrammen.

Histogrammen

De histogrammen die we nodig hebben, zijn gekoppeld aan de CurrencyKey kolom op elke samengevoegde tabel. Op een nieuwe kopie van de AdventureWorksDW-database, de reeds bestaande statistieken voor de grotere FactResellerSales tabellen zijn gebaseerd op een steekproef. Om de reproduceerbaarheid te maximaliseren en de gedetailleerde berekeningen zo eenvoudig mogelijk te maken (om schalen te vermijden), zullen we eerst de statistieken vernieuwen met een volledige scan:

UPDATE STATISTICS dbo.FactCurrencyRate WITH FULLSCAN;
UPDATE STATISTICS dbo.FactResellerSales WITH FULLSCAN;

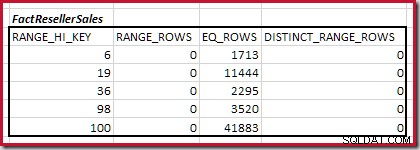
Deze tabellen hebben het demovriendelijke voordeel dat ze kleine en eenvoudige maxdiff . maken histogrammen:

DBCC SHOW_STATISTICS
    (FactResellerSales, CurrencyKey)
WITH HISTOGRAM;
 
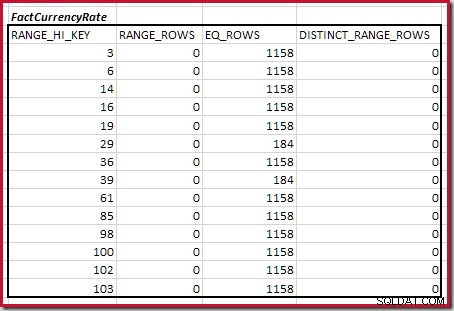
DBCC SHOW_STATISTICS
    (FactCurrencyRate, [PK_FactCurrencyRate_CurrencyKey_DateKey])
WITH HISTOGRAM;

Minimaal overeenkomende histogramstappen combineren

De eerste stap in de grove uitlijning berekening is om de bijdrage aan de join-kardinaliteit te vinden die wordt geleverd door de laagste overeenkomende histogramstap. Voor onze voorbeeldhistogrammen is de minimale overeenkomende stapwaarde RANGE_HI_KEY = 6 :

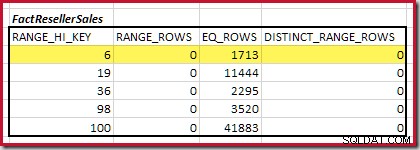
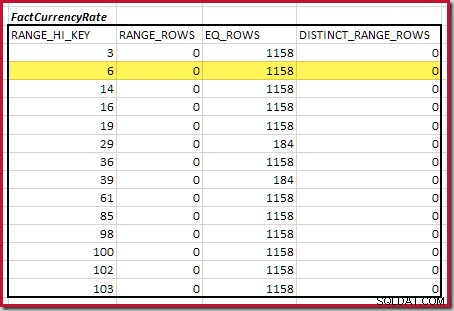
De geschatte equijoin-kardinaliteit voor alleen deze gemarkeerde stap is 1.713 * 1.158 =1.983.654 rijen .

Resterende overeenkomende stappen

Vervolgens moeten we het bereik van het histogram RANGE_HI_KEY . identificeren stappen op tot het maximum voor mogelijke equijoin-overeenkomsten. Dit houdt in dat u vooruitgaat vanaf het eerder gevonden minimum totdat een van de histograminvoer geen rijen meer heeft. De overeenkomende equijoin-bereiken voor het huidige voorbeeld worden hieronder gemarkeerd:

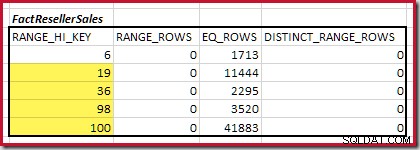
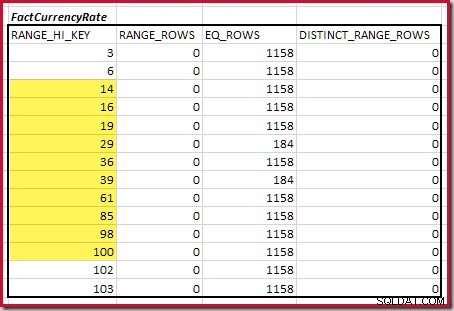
Deze twee bereiken vertegenwoordigen de resterende rijen waarvan kan worden verwacht dat ze bijdragen aan equijoin-kardinaliteit.

Grove, op frequentie gebaseerde schatting

De vraag is nu hoe je een grove . uitvoert schatting van de equijoin-kardinaliteit van de gemarkeerde stappen, met behulp van de beschikbare informatie.

De oorspronkelijke kardinaliteitsschatter zou een fijnkorrelige stapsgewijze histogramuitlijning hebben uitgevoerd met behulp van lineaire interpolatie, de join-bijdrage van elke stap hebben beoordeeld (zoals we eerder deden voor de minimale stapwaarde), en elke stapbijdrage hebben opgeteld om een volledige deelname schatting. Hoewel deze procedure intuïtief heel logisch is, was de praktijkervaring dat deze fijnmazige benadering rekenkundige overhead toevoegde en resultaten van variabele kwaliteit kon opleveren.

De oorspronkelijke schatter had een andere manier om de join-kardinaliteit te schatten wanneer histograminformatie niet beschikbaar was of heuristisch als inferieur werd beoordeeld. Dit staat bekend als een op frequentie gebaseerde schatting en gebruikt de volgende definities:

• C – de kardinaliteit (aantal rijen)
• D – het aantal verschillende waarden
• F – de frequentie (aantal rijen) voor elke afzonderlijke waarde
• Noot C =D * F per definitie

Het effect van een equijoin van relaties R1 en R2 op elk van deze eigenschappen is als volgt:

• F' =F1 * F2
• D' =MIN(D1; D2) – uitgaande van insluiting
• C' =D' * F' (alweer, per definitie)

We zitten achter C', de kardinaliteit van de equijoin. Vervangen van D' en F' in de formule, en uitbreiden:

• C' =D' * F'
• C' =MIN(D1; D2) * F1 * F2
• C' =MIN(D1 * F1 * F2; D2 * F1 * F2)
• nu, aangezien C1 =D1 * F1 en C2 =D2 * F2:
• C' =MIN(C1 * F2, C2 * F1)
• tot slot, aangezien F =C/D (ook per definitie):
• C' =MIN(C1 * C2 / D2; C2 * C1 / D1)

Opmerkend dat C1 * C2 het product is van de twee invoerkardinaliteiten (Cartesiaanse join), is het duidelijk dat het minimum van die uitdrukkingen degene zal zijn met het hoogste aantal verschillende waarden:

• C' =(C1 * C2) / MAX(D1; D2)

In het geval dat dit allemaal een beetje abstract lijkt, is een intuïtieve manier om na te denken over op frequentie gebaseerde equijoin-schatting, te overwegen dat elke afzonderlijke waarde van de ene relatie samenkomt met een aantal rijen (de gemiddelde frequentie) in de andere relatie. Als we aan de ene kant 5 verschillende waarden hebben en elke afzonderlijke waarde aan de andere kant komt gemiddeld 3 keer voor, dan is een verstandige (maar grove) equijoin-schatting 5 * 3 =15.

Dit is niet zo'n brede borstel als het lijkt. Onthoud dat de kardinaliteit en verschillende waarden hierboven niet uit de hele relatie komen, maar alleen uit de overeenkomende stappen boven het minimum. Vandaar een grove schatting tussen minimum- en maximumwaarden.

Frequentieberekening

We kunnen elk van deze parameters uit de gemarkeerde histogramstappen halen.

• De kardinaliteit C is de som van EQ_ROWS en RANGE_ROWS .
• Het aantal verschillende waarden D is de som van DISTINCT_RANGE_ROWS plus één voor elke stap.

De kardinaliteit C1 van overeenkomende FactResellerSales stappen is de som van de gemarkeerde cellen:

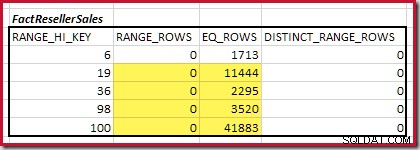
Dit geeft C1 =59.142 rijen.

Er zijn geen afzonderlijke bereikrijen, dus de enige afzonderlijke waarden komen van de vier stapgrenzen zelf, waardoor D1 =4 .

Voor de tweede tafel:

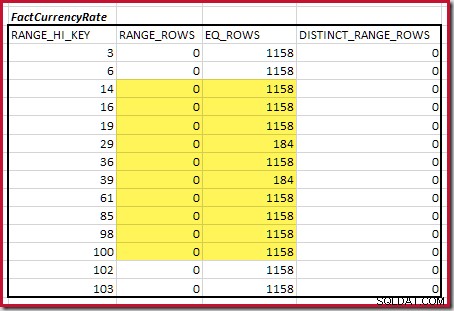
Dit geeft C2 =9.632 . Nogmaals, er zijn geen afzonderlijke bereikrijen, dus de afzonderlijke waarden komen uit de tien-stapsgrenzen, D2 =10.

De schatting van Equijoin voltooien

We hebben nu alle getallen die we nodig hebben voor de equijoin-formule:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(59142 * 9632) / MAX(4; 10)
• C' =569655744 / 10
• C' =56.965.574,4

Onthoud dat dit de bijdrage is van de histogramstappen boven de minimaal overeenkomende grens. Om de schatting van de join-kardinaliteit te voltooien, moeten we de bijdrage van de minimale overeenkomende stapwaarden toevoegen, namelijk 1.713 * 1.158 =1.983.654 rijen.

De uiteindelijke schatting van equijoin is daarom 56.965.574,4 + 1.983.654 =58.949.228,4 rijen of 58.949.200 tot zes significante cijfers.

Dit resultaat wordt bevestigd in het geschatte uitvoeringsplan voor de bronquery:

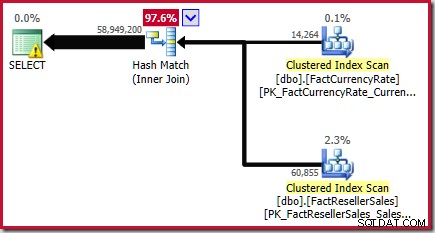
Zoals opgemerkt in het Witboek, is dit geen geweldige schatting. Het werkelijke aantal rijen dat door deze zoekopdracht wordt geretourneerd, is 70.470.090 . De schatting die is geproduceerd door de originele ("legacy") kardinaliteitsschatter - met behulp van stapsgewijze histogramuitlijning - is 70.470.100 rijen.

Met de fijnere methode zijn vaak betere resultaten mogelijk, maar alleen als de statistieken een zeer goede weergave zijn van de onderliggende datadistributie. Dit is niet alleen een kwestie van statistieken up-to-date houden of volledige scanpopulatie gebruiken. Het algoritme dat wordt gebruikt om informatie in maximaal 201 histogramstappen in te pakken is niet perfect, en in elk geval zijn veel real-world datadistributies eenvoudig niet in staat tot een dergelijke histogramgetrouwheid. Gemiddeld zouden mensen moeten ontdekken dat de grovere methode perfect passende schattingen en meer stabiliteit geeft met de nieuwe CE.

Tweede voorbeeld

Dit bouwt een beetje voort op het vorige voorbeeld en vereist geen download van een voorbeelddatabase.

DROP TABLE IF EXISTS
    dbo.R1,
    dbo.R2;
 
CREATE TABLE dbo.R1 (n integer NOT NULL);
CREATE TABLE dbo.R2 (n integer NOT NULL);
 
INSERT dbo.R1
    (n)
VALUES
    (1), (2), (3), (4), (5), (6), (7), (8), (9), (10),
    (6), (6), (6), (6), (6), (6), (6), (6), (6), (6), 
    (6), (6), (6), (6), (6), (6), (6), (6), (6);
 
INSERT dbo.R2
    (n)
VALUES
    (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15),
    (10), (10);
 
CREATE STATISTICS stats_n ON dbo.R1 (n) WITH FULLSCAN;
CREATE STATISTICS stats_n ON dbo.R2 (n) WITH FULLSCAN;

De histogrammen met overeenkomende minimale stappen zijn:

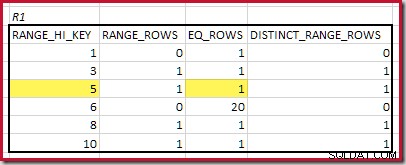
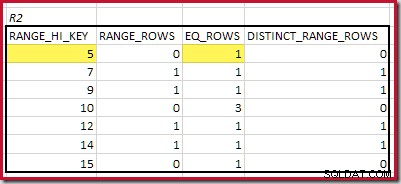
De laagste RANGE_HI_KEY die overeenkomt is 5. De waarde van EQ_ROWS is 1 in beide, dus de geschatte equijoin-kardinaliteit is 1 * 1 =1 rij .

De best overeenkomende RANGE_HI_KEY is 10. Markering van de R1-histogramrijen voor grove frequentiegebaseerde schatting:

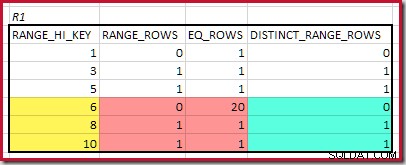
Optellen van EQ_ROWS en RANGE_ROWS geeft C1 =24 . Het aantal verschillende rijen is 2 DISTINCT_RANGE_ROWS (verschillende waarden tussen stappen) plus 3 voor de verschillende waarden die bij elke stapgrens horen, wat D1 =5 geeft .

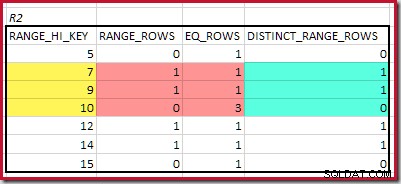
Voor R2 optellen van EQ_ROWS en RANGE_ROWS geeft C2 =7 . Het aantal verschillende rijen is 2 DISTINCT_RANGE_ROWS (verschillende waarden tussen stappen) plus 3 voor de verschillende waarden die bij elke stapgrens horen, wat D2 =5 geeft .

De equijoin schatting C' is:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(24 * 7) / 5
• C' =33,6

Toevoegen in de 1 rij uit de minimale stapovereenkomst geeft een totale schatting van 34,6 rijen voor de equijoin:

SELECT
    R1.n,
    R2.n
FROM dbo.R1 AS R1
JOIN dbo.R2 AS R2
    ON R2.n = R1.n;

Het geschatte uitvoeringsplan toont een schatting die overeenkomt met onze berekening:

Dit is niet helemaal juist, maar de "oude" kardinaliteitsschatter doet het niet beter, met een schatting van 15,25 rijen versus 27 werkelijke:

Voor een volledige behandeling zouden we ook een laatste bijdrage moeten toevoegen van overeenkomende histogram-nulstappen, maar dit is ongebruikelijk voor equijoins (die meestal worden geschreven om nulls te verwerpen) en een relatief eenvoudige uitbreiding voor de geïnteresseerde lezer.

Laatste gedachten

Hopelijk vullen de details in het artikel een paar hiaten op voor iedereen die zich ooit heeft afgevraagd wat 'grove uitlijning' is. Merk op dat dit slechts een klein onderdeel is in de kardinaliteitsschatter. Er zijn verschillende andere belangrijke concepten en algoritmen die worden gebruikt voor het schatten van joins, met name de manier waarop niet-join-predikaten worden beoordeeld en hoe complexere joins worden afgehandeld. Veel van de echt belangrijke stukjes worden redelijk goed behandeld in het Witboek.