Terugkerende combinaties
Gebruik een getallentabel of nummergenererende CTE, selecteer 0 tot en met 2^n - 1. Gebruik de bitposities die 1s in deze getallen bevatten om de aan- of afwezigheid van de relatieve leden in de combinatie aan te geven, en elimineer die welke dat niet hebben het juiste aantal waarden, moet u een resultatenset kunnen retourneren met alle gewenste combinaties.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Deze query presteert redelijk goed, maar ik heb een manier bedacht om deze te optimaliseren, cribbing van de Handige parallelle bittelling om eerst het juiste aantal items tegelijk te nemen. Dit presteert 3 tot 3,5 keer sneller (zowel CPU als tijd):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Ik ging en las de pagina over het tellen van bits en dacht dat dit beter zou kunnen presteren als ik niet de % 255 zou doen, maar de hele weg zou gaan met het rekenen met bits. Als ik de kans krijg, zal ik dat proberen en kijken hoe het werkt.
Mijn prestatieclaims zijn gebaseerd op de query's die worden uitgevoerd zonder de ORDER BY-clausule. Voor de duidelijkheid:wat deze code doet, is het aantal set 1-bits tellen in Num van de Numbers tafel. Dat komt omdat het nummer wordt gebruikt als een soort indexeerder om te kiezen welke elementen van de set in de huidige combinatie zitten, dus het aantal 1-bits zal hetzelfde zijn.
Ik hoop dat je het leuk vindt!
Voor de goede orde, deze techniek om het bitpatroon van gehele getallen te gebruiken om leden van een set te selecteren, is wat ik de "Vertical Cross Join" heb bedacht. Het resulteert in feite in de cross-join van meerdere datasets, waarbij het aantal sets &cross-joins willekeurig is. Hier is het aantal sets het aantal items dat tegelijkertijd wordt genomen.
In feite zou cross-joining in de gebruikelijke horizontale zin (van het toevoegen van meer kolommen aan de bestaande lijst met kolommen bij elke join) er ongeveer zo uitzien:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Mijn bovenstaande vragen "cross join" zo vaak als nodig is met slechts één join. De resultaten zijn niet gedraaid in vergelijking met echte kruiskoppelingen, zeker, maar dat is van ondergeschikt belang.
Kritiek van uw code
Mag ik ten eerste deze wijziging in uw Factorial UDF voorstellen:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Nu kunt u veel grotere reeksen combinaties berekenen, en bovendien is het efficiënter. Je zou zelfs kunnen overwegen om decimal(38, 0) . te gebruiken om grotere tussentijdse berekeningen in uw combinatieberekeningen toe te staan.
Ten tweede levert uw opgegeven zoekopdracht niet de juiste resultaten op. Als ik bijvoorbeeld mijn testgegevens van de onderstaande prestatietests gebruik, is set 1 hetzelfde als set 18. Het lijkt erop dat uw zoekopdracht een glijdende streep heeft die zich eromheen wikkelt:elke set bestaat altijd uit 5 aangrenzende leden, die er ongeveer zo uitzien (ik draaide om het gemakkelijker te maken om te zien):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Vergelijk het patroon van mijn vragen:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Om het bitpatroon -> index van combinatie-dingen naar huis te sturen voor iedereen die geïnteresseerd is, merk op dat 31 in binair =11111 en het patroon ABCDE is. 121 in binair is 1111001 en het patroon is A__DEFG (achterwaarts in kaart gebracht).
Prestatieresultaten met een tabel met reële getallen
Ik heb wat prestatietests uitgevoerd met grote sets op mijn tweede vraag hierboven. Ik heb op dit moment geen record van de gebruikte serverversie. Dit zijn mijn testgegevens:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter toonde aan dat deze "verticale cross join" niet zo goed presteert als het simpelweg schrijven van dynamische SQL om de CROSS JOIN's die het vermijdt uit te voeren. Tegen de triviale prijs van nog een paar keer lezen, heeft zijn oplossing statistieken die tussen de 10 en 17 keer beter zijn. De prestaties van zijn zoekopdracht nemen sneller af dan de mijne naarmate de hoeveelheid werk toeneemt, maar niet snel genoeg om te voorkomen dat iemand het gebruikt.
De tweede reeks getallen hieronder is de factor gedeeld door de eerste rij in de tabel, om te laten zien hoe deze schaalt.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Peter
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Extrapoleren, uiteindelijk zal mijn vraag goedkoper zijn (hoewel het vanaf het begin in reads is), maar niet voor een lange tijd. Om 21 items in de set te gebruiken, heb je al een getallentabel nodig die oploopt tot 2097152...
Hier is een opmerking die ik oorspronkelijk maakte voordat ik me realiseerde dat mijn oplossing drastisch beter zou presteren met een on-the-fly getallentabel:
Prestatieresultaten met een on-the-fly getallentabel
Toen ik dit antwoord oorspronkelijk schreef, zei ik:
Nou, ik heb het geprobeerd, en de resultaten waren dat het veel beter presteerde! Dit is de zoekopdracht die ik heb gebruikt:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Merk op dat ik de waarden in variabelen heb geselecteerd om de tijd en het geheugen te verminderen die nodig zijn om alles te testen. De server doet nog steeds hetzelfde werk. Ik heb de versie van Peter aangepast zodat deze vergelijkbaar is en onnodige extra's verwijderd, zodat ze allebei zo slank mogelijk waren. De serverversie die voor deze tests wordt gebruikt, is Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) draait op een VM.
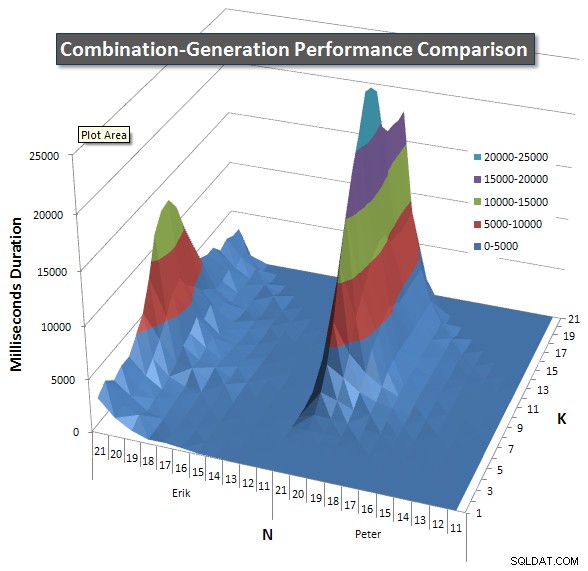
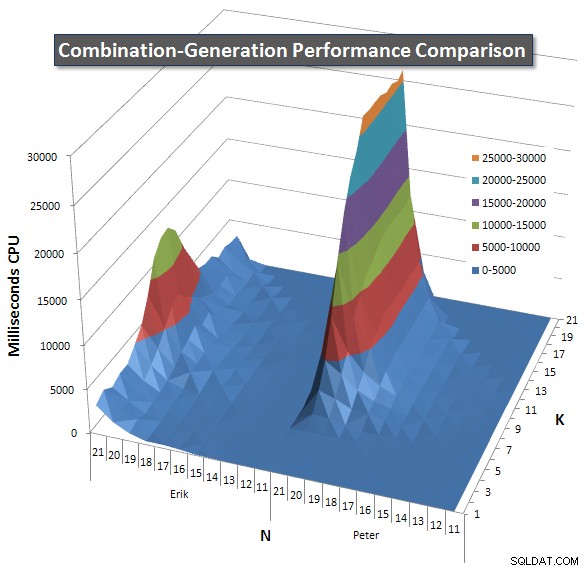
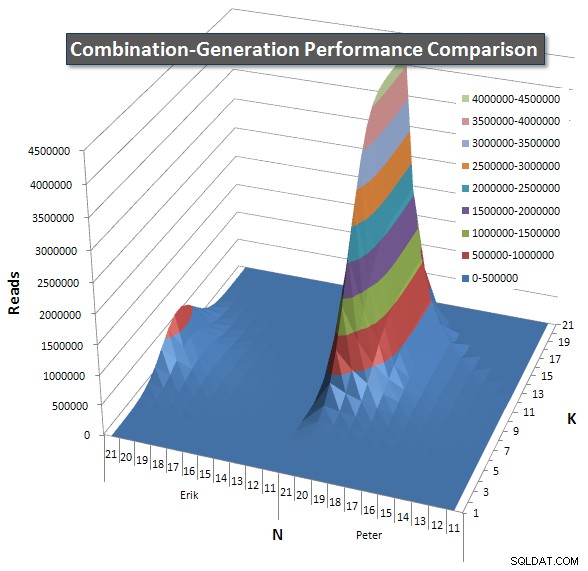
Hieronder staan grafieken met de prestatiecurven voor waarden van N en K tot 21. De basisgegevens daarvoor staan in een ander antwoord op deze pagina . De waarden zijn het resultaat van 5 uitvoeringen van elke zoekopdracht bij elke K- en N-waarde, gevolgd door het weggooien van de beste en slechtste waarden voor elke statistiek en het middelen van de resterende 3.
Kortom, mijn versie heeft een "schouder" (in de meest linkse hoek van de grafiek) bij hoge waarden van N en lage waarden van K waardoor het daar slechter presteert dan de dynamische SQL-versie. Dit blijft echter vrij laag en constant, en de centrale piek rond N =21 en K =11 is veel lager voor Duur, CPU en Reads dan de dynamische SQL-versie.
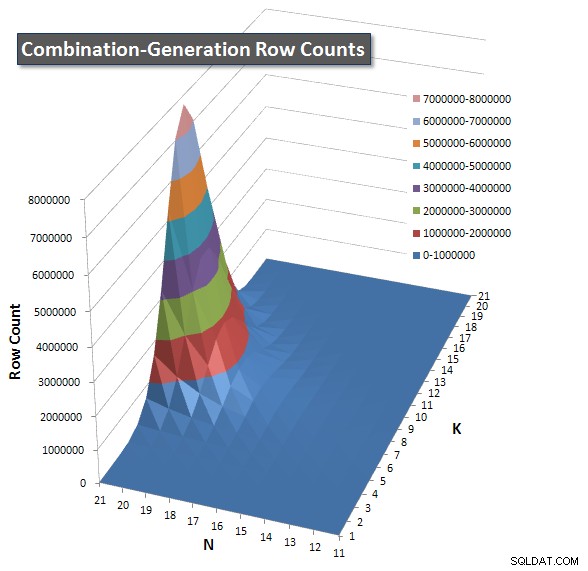
Ik heb een diagram toegevoegd met het aantal rijen dat elk item naar verwachting zal retourneren, zodat u kunt zien hoe de zoekopdracht presteert in vergelijking met de grote taak die het moet uitvoeren.
Zie mijn aanvullende antwoord op deze pagina voor de volledige prestatieresultaten. Ik heb de posttekenlimiet bereikt en kon deze hier niet opnemen. (Enig idee waar het anders te plaatsen?) Om dingen in perspectief te plaatsen tegen de prestatieresultaten van mijn eerste versie, hier is hetzelfde formaat als voorheen:
Erik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Peter
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Conclusies
- Tabels met on-the-fly getallen zijn beter dan een echte tabel met rijen, aangezien het lezen van een tabel met enorme rijen veel I/O vereist. Het is beter om een kleine CPU te gebruiken.
- Mijn eerste tests waren niet breed genoeg om de prestatiekenmerken van de twee versies echt te laten zien.
- Peter's versie kan worden verbeterd door elke JOIN niet alleen groter te maken dan het vorige item, maar ook de maximale waarde te beperken op basis van hoeveel meer items in de set moeten passen. Bijvoorbeeld, bij 21 items die met 21 tegelijk zijn genomen, is er slechts één antwoord van 21 rijen (alle 21 items, één keer), maar de tussenliggende rijensets in de dynamische SQL-versie, vroeg in het uitvoeringsplan, bevatten combinaties zoals " AU" bij stap 2, hoewel dit bij de volgende join wordt weggegooid omdat er geen hogere waarde dan "U" beschikbaar is. Evenzo zal een tussenliggende rijenset bij stap 5 "ARSTU" bevatten, maar de enige geldige combo op dit punt is "ABCDE". Deze verbeterde versie zou geen lagere piek in het midden hebben, dus mogelijk niet voldoende verbeteren om de duidelijke winnaar te worden, maar het zou in ieder geval symmetrisch worden zodat de grafieken niet tot voorbij het midden van de regio zouden blijven, maar terug zouden vallen tot bijna 0 zoals mijn versie doet (zie de bovenhoek van de pieken voor elke zoekopdracht).
Duuranalyse
- Er is geen echt significant verschil tussen de versies in duur (>100 ms) tot 14 items met 12 tegelijk. Tot nu toe wint mijn versie 30 keer en de dynamische SQL-versie 43 keer.
- Vanaf 14•12 was mijn versie 65 keer sneller (59>100 ms), de dynamische SQL-versie 64 keer (60>100 ms). Maar al die keren dat mijn versie sneller was, bespaarde het een totale gemiddelde duur van 256,5 seconden, en toen de dynamische SQL-versie sneller was, bespaarde het 80,2 seconden.
- De totale gemiddelde duur voor alle proeven was Erik 270,3 seconden, Peter 446,2 seconden.
- Als er een opzoektabel zou zijn gemaakt om te bepalen welke versie moet worden gebruikt (door de snellere voor de invoer te kiezen), zouden alle resultaten in 188,7 seconden kunnen worden uitgevoerd. Elke keer de langzaamste gebruiken zou 527,7 seconden duren.
Lees Analyse
De duuranalyse toonde aan dat mijn zoekopdracht aanzienlijk maar niet overdreven veel won. Wanneer de statistiek wordt overgeschakeld naar leest, komt er een heel ander beeld naar voren:mijn zoekopdracht gebruikt gemiddeld 1/10e van de lezingen.
- Er is geen echt significant verschil tussen de versies in reads (>1000) tot 9 items met 9 tegelijk. Tot nu toe wint mijn versie 30 keer en de dynamische SQL-versie 17 keer.
- Vanaf 9•9 gebruikte mijn versie 118 keer minder reads (113>1000), de dynamische SQL-versie 69 keer (31>1000). Maar al die keren dat mijn versie minder reads gebruikte, bespaarde het in totaal gemiddeld 75,9 miljoen reads, en toen de dynamische SQL-versie sneller was, bespaarde het 380K reads.
- Het totale gemiddelde aantal metingen voor alle proeven was Erik 8,4 miljoen, Peter 84 miljoen.
- Als er een opzoektabel zou zijn gemaakt om te bepalen welke versie moet worden gebruikt (door de beste voor de invoer te kiezen), kunnen alle resultaten worden uitgevoerd in 8M-uitlezingen. Elke keer de slechtste gebruiken zou 84,3 miljoen leesacties vergen.
Ik zou graag de resultaten zien van een bijgewerkte dynamische SQL-versie die de extra bovengrens stelt voor de items die bij elke stap zijn gekozen, zoals ik hierboven heb beschreven.
Aanvulling
De volgende versie van mijn query behaalt een verbetering van ongeveer 2,25% ten opzichte van de hierboven vermelde prestatieresultaten. Ik heb de HAKMEM-bittelmethode van MIT gebruikt en een Convert(int) toegevoegd op het resultaat van row_number() omdat het een bigint teruggeeft. Natuurlijk zou ik willen dat dit de versie was die ik had gebruikt voor alle prestatietests en grafieken en gegevens hierboven, maar het is onwaarschijnlijk dat ik het ooit opnieuw zal doen omdat het arbeidsintensief was.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
En ik kon het niet laten om nog een versie te laten zien die een opzoeking doet om het aantal bits te krijgen. Het kan zelfs sneller zijn dan andere versies:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))
