Vraag en aanbod afstemmen - Oplossingen, deel 2

[ Ga naar:Originele uitdaging | Oplossingen:Deel 1 | Deel 2 | Deel 3 ]

In dit artikel ga ik verder met de dekking van oplossingen voor Peter Larssons verleidelijke uitdaging om vraag en aanbod op elkaar af te stemmen. Nogmaals bedankt aan Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie en Peter Larsson voor het sturen van jullie oplossingen.

Vorige maand heb ik een oplossing behandeld op basis van intervalintersecties, met behulp van een klassieke op predikaten gebaseerde intervalintersectietest. Ik noem die oplossing klassieke kruispunten . De klassieke benadering van intervalkruisingen resulteert in een plan met kwadratische schaling (N^2). Ik demonstreerde zijn slechte prestaties tegen voorbeeldinvoer variërend van 100K tot 400K rijen. Het kostte de oplossing 931 seconden om te voltooien tegen de invoer van 400K rijen! Deze maand zal ik beginnen met u kort te herinneren aan de oplossing van vorige maand en waarom deze zo slecht schaalt en presteert. Ik zal dan een aanpak introduceren op basis van een herziening van de intervalintersectietest. Deze aanpak werd gebruikt door Luca, Kamil en mogelijk ook Daniel, en het maakt een oplossing mogelijk met veel betere prestaties en schaalbaarheid. Ik noem die oplossing herziene kruispunten .

Het probleem met de klassieke kruisingstest

Laten we beginnen met een snelle herinnering aan de oplossing van vorige maand.

Ik heb de volgende indexen gebruikt in de invoer-dbo.Auctions-tabel ter ondersteuning van de berekening van de lopende totalen die de vraag- en aanbodintervallen produceren:

-- Index to support solution
 
CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);
 
-- Enable batch-mode Window Aggregate
 
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

De volgende code heeft de complete oplossing die de klassieke benadering van intervallen van intervallen implementeert:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

Deze code begint met het berekenen van de vraag- en aanbodintervallen en schrijft deze naar tijdelijke tabellen met de naam #Demand en #Supply. De code maakt vervolgens een geclusterde index op #Supply met EndSupply als leidende sleutel om de intersectietest zo goed mogelijk te ondersteunen. Ten slotte voegt de code #Supply en #Demand samen, waarbij transacties worden geïdentificeerd als de overlappende segmenten van de kruisende intervallen, met behulp van het volgende join-predikaat op basis van de klassieke interval-intersectietest:

D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

Het plan voor deze oplossing wordt getoond in figuur 1.

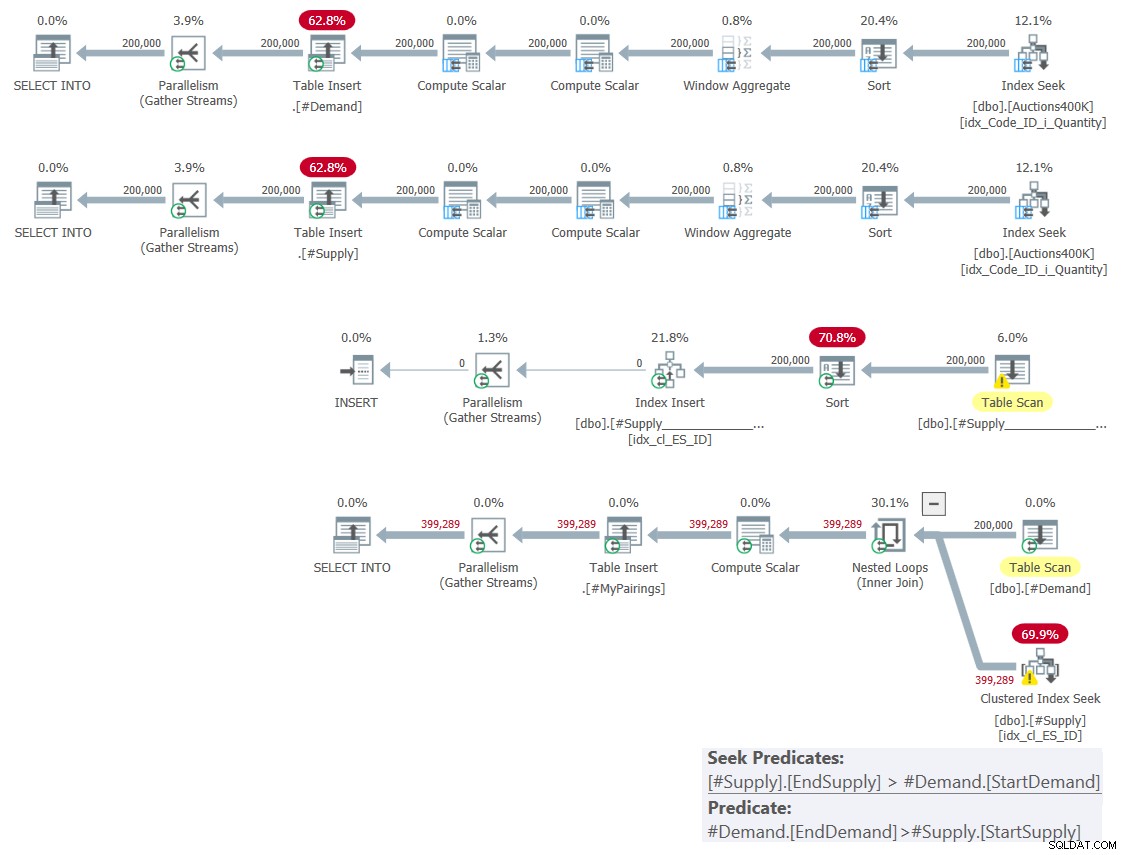Figuur 1:Queryplan voor oplossing op basis van klassieke kruispunten

Zoals ik vorige maand heb uitgelegd, kan van de twee betrokken bereikpredikaten er slechts één worden gebruikt als zoekpredikaat als onderdeel van een indexzoekbewerking, terwijl de andere moet worden toegepast als een residuaal predikaat. Je kunt dit duidelijk zien in het plan voor de laatste query in figuur 1. Daarom heb ik maar de moeite genomen om één index op een van de tabellen te maken. Ik heb ook het gebruik van een zoekopdracht afgedwongen in de index die ik heb gemaakt met behulp van de FORCESEEK-hint. Anders zou de optimizer die index kunnen negeren en er zelf een kunnen maken met behulp van een Index Spool-operator.

Dit plan heeft kwadratische complexiteit, aangezien per rij aan de ene kant - # Vraag in ons geval - de indexzoekopdracht gemiddeld de helft van de rijen aan de andere kant moet openen - # Aanbod in ons geval - op basis van het zoekpredikaat en de laatste wedstrijden door het resterende predikaat toe te passen.

Als het je nog steeds niet duidelijk is waarom dit plan kwadratische complexiteit heeft, kan een visuele weergave van het werk misschien helpen, zoals weergegeven in figuur 2.

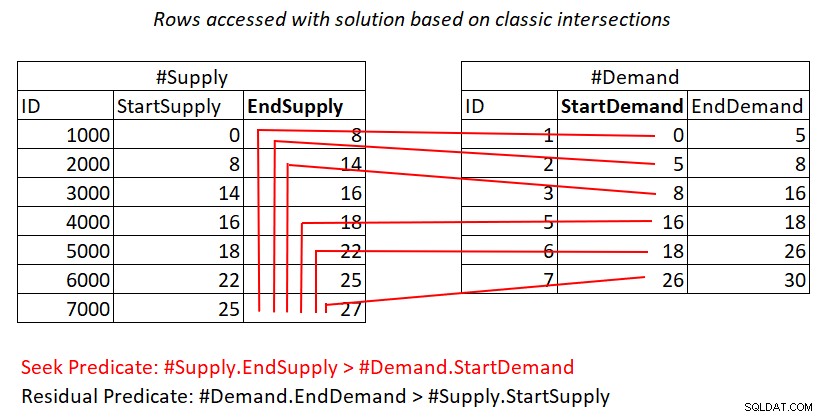Figuur 2:Illustratie van werk met een oplossing op basis van klassieke kruispunten

Deze illustratie geeft het werk weer dat is gedaan door de Nested Loops join in het plan voor de laatste query. De #Demand-heap is de buitenste invoer van de join en de geclusterde index op #Supply (met EndSupply als leidende sleutel) is de binnenste invoer. De rode lijnen vertegenwoordigen de indexzoekactiviteiten per rij in #Demand in de index op #Supply en de rijen die ze openen als onderdeel van de bereikscans in het indexblad. Op weg naar extreem lage StartDemand-waarden in #Demand, moet de bereikscan toegang hebben tot bijna alle rijen in #Supply. Op weg naar extreem hoge StartDemand-waarden in #Demand, moet de bereikscan toegang hebben tot bijna nul rijen in #Supply. Gemiddeld heeft de bereikscan toegang nodig tot ongeveer de helft van de rijen in #Aanvoer per gevraagde rij. Bij D vraagrijen en S aanbodrijen is het aantal toegankelijke rijen D + D*S/2. Dat komt bovenop de kosten van de zoekopdrachten die u naar de overeenkomende rijen brengen. Als u bijvoorbeeld dbo.Auctions vult met 200.000 vraagrijen en 200.000 aanbodsrijen, vertaalt dit zich naar de Nested Loops join die toegang heeft tot 200.000 vraagrijen + 200.000*200.000/2 aanbodsrijen, of 200.000 + 200.000^2/2 =20.000.200.000 rijen die zijn geopend. Er vindt hier veel herscanning van aanbodrijen plaats!

Als je je aan het idee van intervalkruisingen wilt houden, maar goede prestaties wilt leveren, moet je een manier bedenken om de hoeveelheid werk te verminderen.

In zijn oplossing heeft Joe Obbish de intervallen gebucketiseerd op basis van de maximale intervallengte. Op deze manier kon hij het aantal rijen verminderen dat de joins nodig hadden om batchverwerking te verwerken en erop te vertrouwen. Hij gebruikte de klassieke intervalintersectietest als een laatste filter. De oplossing van Joe werkt goed zolang de maximale intervallengte niet erg hoog is, maar de runtime van de oplossing neemt toe naarmate de maximale intervallengte toeneemt.

Dus, wat kun je nog meer doen...?

Herziene kruispunttest

Luca, Kamil en mogelijk Daniel (er was een onduidelijk deel over zijn geposte oplossing vanwege de opmaak van de website, dus ik moest raden) gebruikten een herziene intervalintersectietest die een veel beter gebruik van indexering mogelijk maakt.

Hun intersectietest is een disjunctie van twee predikaten (predikaten gescheiden door OR-operator):

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

In het Engels kruist ofwel de vraagstartbegrenzer het aanbodinterval op een inclusieve, exclusieve manier (inclusief het begin en exclusief het einde); of het begrenzingsteken voor het begin van het aanbod kruist het vraaginterval, op een inclusieve, exclusieve manier. Om de twee predikaten onsamenhangend te maken (geen overlappende naamvallen hebben) maar toch volledig zijn in het dekken van alle gevallen, kunt u de operator =in de een of de ander houden, bijvoorbeeld:

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

Deze herziene intervalintersectietest is behoorlijk inzichtelijk. Elk van de predikaten kan potentieel efficiënt een index gebruiken. Overweeg predikaat 1:

D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Ervan uitgaande dat u een dekkingsindex maakt op #Demand met StartDemand als leidende sleutel, kunt u mogelijk een Nested Loops-join krijgen door het werk toe te passen dat wordt geïllustreerd in Afbeelding 3.

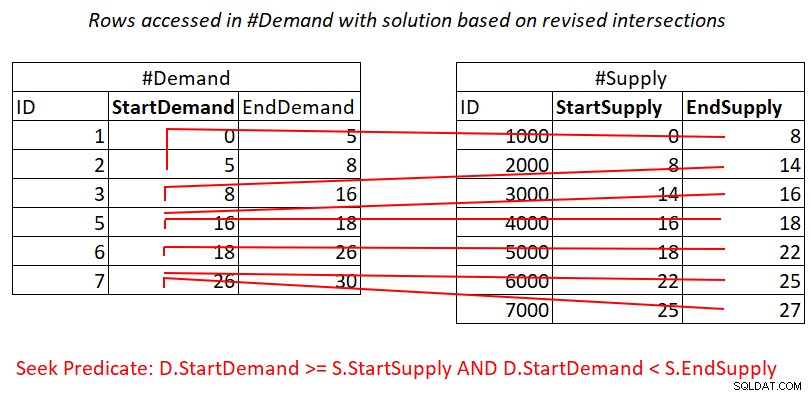
Figuur 3:Illustratie van theoretisch werk dat nodig is om het predikaat te verwerken 1

Ja, je betaalt nog steeds voor een zoekopdracht in de #Demand-index per rij in #Supply, maar de bereikscans in het indexblad benaderen bijna onsamenhangende subsets van rijen. Geen herscannen van rijen!

De situatie is vergelijkbaar met predikaat 2:

S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Ervan uitgaande dat u een dekkingsindex maakt op #Supply met StartSupply als leidende sleutel, kunt u mogelijk een Nested Loops-join krijgen door het werk toe te passen dat wordt geïllustreerd in Afbeelding 4.

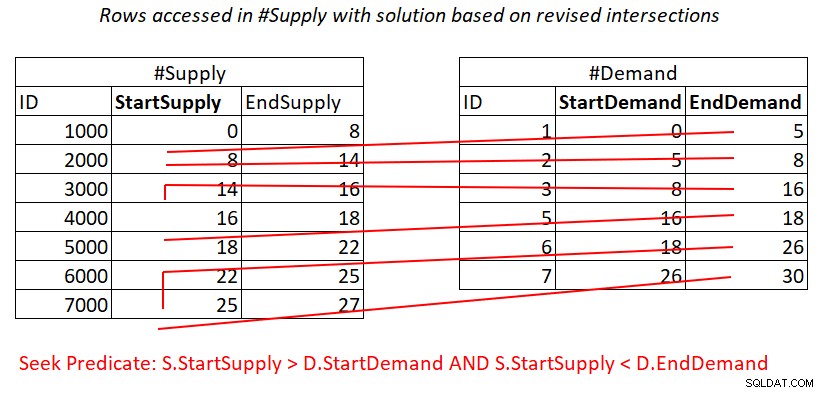
Figuur 4:Illustratie van theoretisch werk dat nodig is om het predikaat te verwerken 2

Ook hier betaal je voor een zoekopdracht in de #Supply-index per rij in #Demand, en dan scant het bereik in het indexblad toegang tot bijna onsamenhangende subsets van rijen. Nogmaals, geen herscannen van rijen!

Uitgaande van D vraagrijen en S aanbodrijen, kan het werk worden beschreven als:

Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

Dus waarschijnlijk is het grootste deel van de kosten hier de I/O-kosten die met de zoekacties gemoeid zijn. Maar dit deel van het werk heeft een lineaire schaling in vergelijking met de kwadratische schaling van de klassieke intervalintersectiequery.

Natuurlijk moet u rekening houden met de voorlopige kosten van het maken van de index op de tijdelijke tabellen, die n log n schaling hebben vanwege de sortering, maar u betaalt dit deel als een voorbereidend deel van beide oplossingen.

Laten we proberen deze theorie in de praktijk te brengen. Laten we beginnen met het vullen van de #Demand en #supply tijdelijke tabellen met de vraag- en aanbodintervallen (hetzelfde als met de klassieke intervalkruisingen) en het creëren van de ondersteunende indexen:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

De plannen voor het vullen van de tijdelijke tabellen en het maken van de indexen worden getoond in figuur 5.

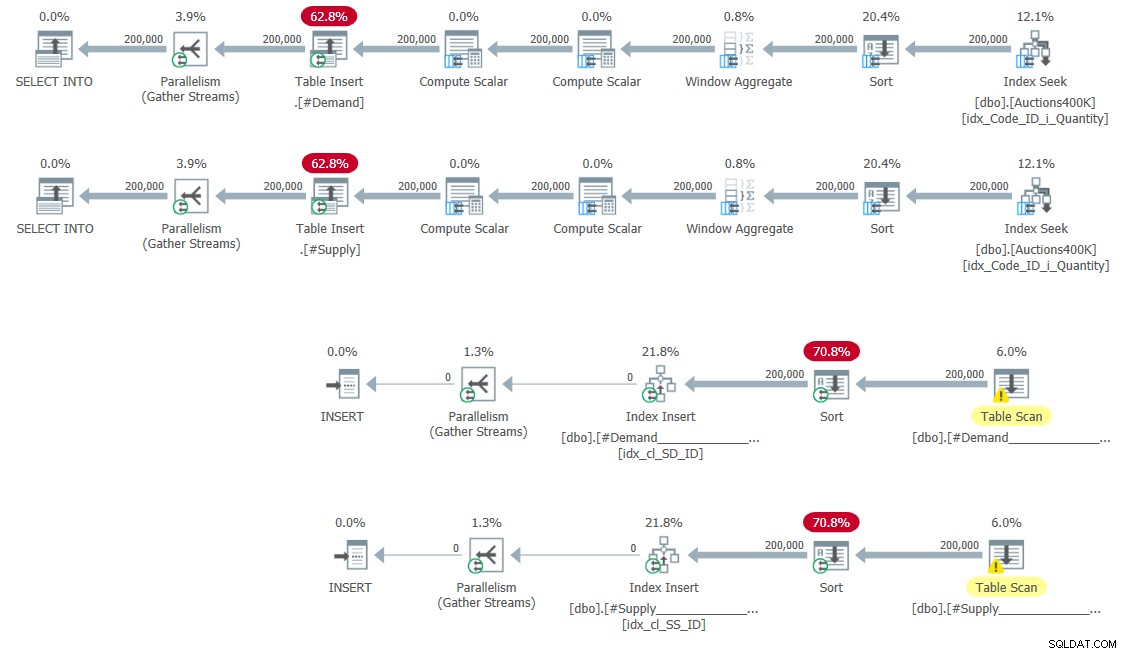
Figuur 5:Queryplannen voor het vullen van tijdelijke tabellen en het maken indexen

Geen verrassingen hier.

Nu naar de laatste vraag. Je zou in de verleiding kunnen komen om een enkele zoekopdracht te gebruiken met de bovengenoemde disjunctie van twee predikaten, zoals:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

Het plan voor deze zoekopdracht wordt getoond in figuur 6.

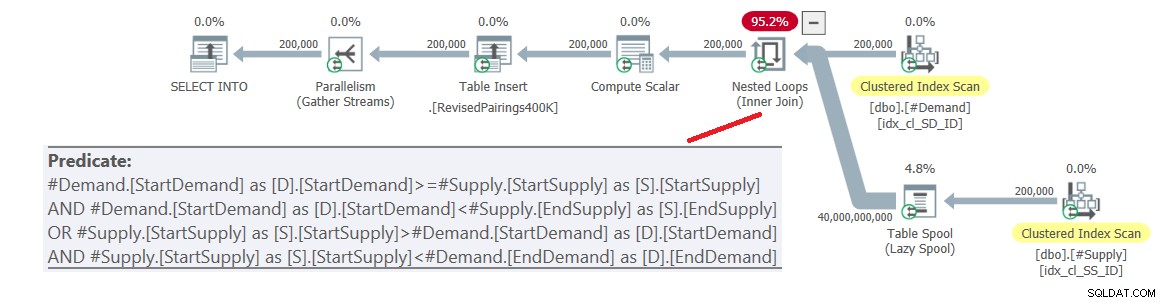
Figuur 6:Queryplan voor definitieve query met herziene intersectie test, probeer 1

Het probleem is dat de optimizer niet weet hoe deze logica in twee afzonderlijke activiteiten moet worden opgesplitst, die elk een ander predikaat hanteren en de respectieve index efficiënt gebruiken. Het eindigt dus met een volledig cartesiaans product van de twee kanten, waarbij alle predikaten als restpredikaten worden toegepast. Met 200.000 vraagrijen en 200.000 aanbodrijen verwerkt de join 40.000.000.000 rijen.

De inzichtelijke truc die door Luca, Kamil en mogelijk Daniel werd gebruikt, was om de logica in twee vragen te splitsen en hun resultaten te verenigen. Dat is waar het gebruik van twee onsamenhangende predikaten belangrijk wordt! U kunt een UNION ALL-operator gebruiken in plaats van UNION, zodat u niet onnodig naar duplicaten hoeft te zoeken. Dit is de query die deze aanpak implementeert:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Het plan voor deze query wordt getoond in figuur 7.

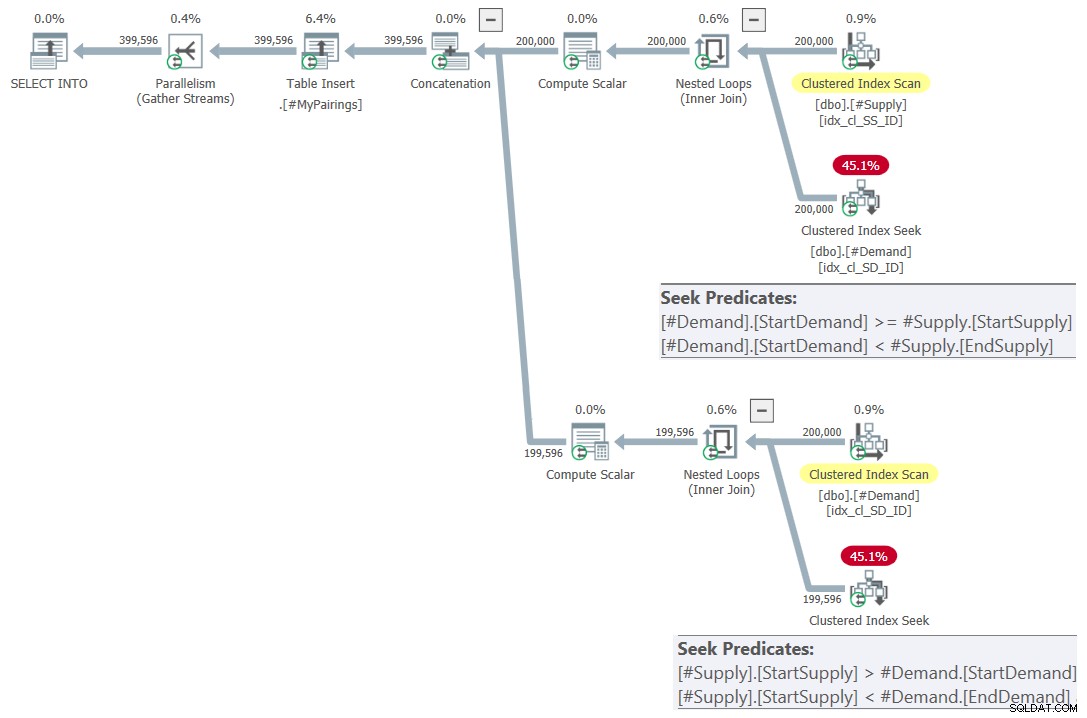
Figuur 7:Queryplan voor definitieve query met herziene intersectie test, probeer 2

Dit is gewoon mooi! Is het niet? En omdat het zo mooi is, volgt hier de volledige oplossing, inclusief het maken van tijdelijke tabellen, indexering en de laatste vraag:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Zoals eerder vermeld, noem ik deze oplossing herziene kruispunten .

Kamils oplossing

Tussen de oplossingen van Luca, Kamil en Daniel was die van Kamil de snelste. Hier is de complete oplossing van Kamil:

SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
 
CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);
 
WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;
 
WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;
 
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;
 
DROP TABLE IF EXISTS #myPairings;
 
CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);
 
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL
 
  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

Zoals je kunt zien, komt het heel dicht in de buurt van de herziene oplossing voor kruispunten die ik heb behandeld.

Het plan voor de laatste vraag in de oplossing van Kamil wordt getoond in figuur 8.

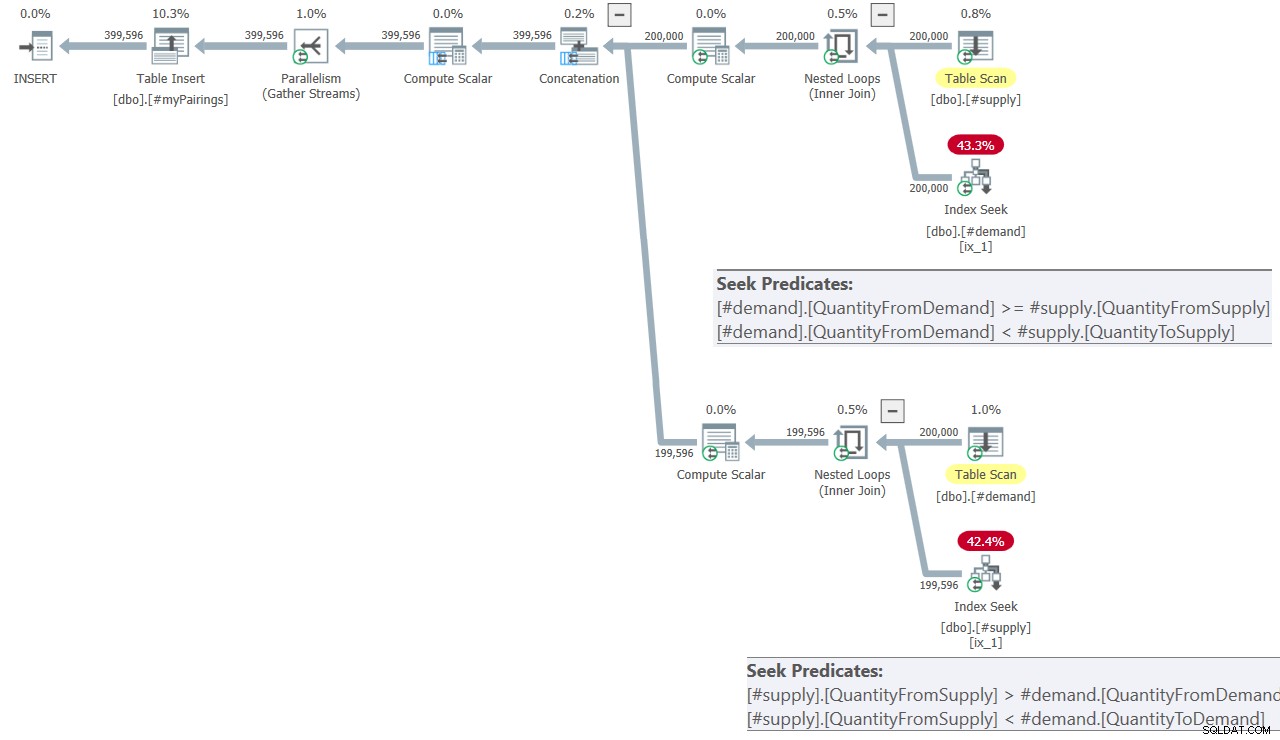
Figuur 8:Queryplan voor de laatste query in de oplossing van Kamil

Het plan lijkt veel op het plan dat eerder in figuur 7 is getoond.

Prestatietest

Bedenk dat de klassieke oplossing voor kruispunten 931 seconden nodig had om te voltooien tegen een invoer met 400K rijen. Dat is 15 minuten! Het is veel, veel erger dan de cursoroplossing, die ongeveer 12 seconden duurde om te voltooien tegen dezelfde invoer. Afbeelding 9 bevat de prestatiecijfers inclusief de nieuwe oplossingen die in dit artikel worden besproken.

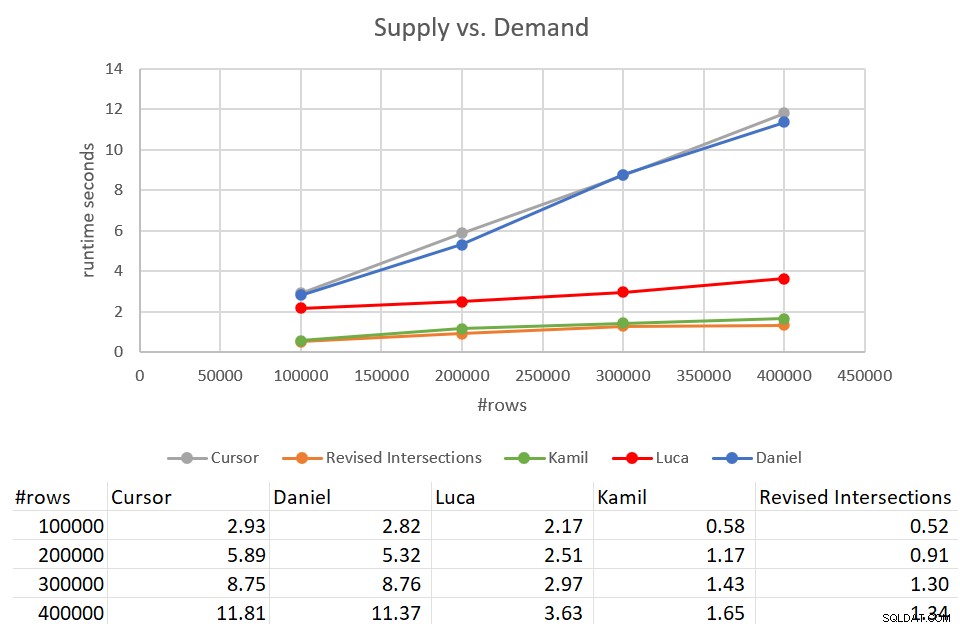
Figuur 9:Prestatietest

Zoals u kunt zien, duurden de oplossing van Kamil en de vergelijkbare herziene oplossing voor kruispunten ongeveer 1,5 seconde om te voltooien tegen de invoer van 400K rijen. Dat is een behoorlijk behoorlijke verbetering in vergelijking met de originele cursorgebaseerde oplossing. Het belangrijkste nadeel van deze oplossingen zijn de I/O-kosten. Met een zoekactie per rij, voor een invoer van 400K rijen, voeren deze oplossingen een overschot van 1,35 miljoen uit. Maar het kan ook als een volkomen acceptabele prijs worden beschouwd, gezien de goede looptijd en schaalvergroting die u krijgt.

Wat nu?

Onze eerste poging om de uitdaging tussen vraag en aanbod op te lossen, was gebaseerd op de klassieke intervalintersectietest en kreeg een slecht presterend plan met kwadratische schaling. Veel erger dan de op cursor gebaseerde oplossing. Gebaseerd op inzichten van Luca, Kamil en Daniel, met behulp van een herziene intervalintersectietest, was onze tweede poging een significante verbetering die indexering efficiënt gebruikt en beter presteert dan de cursorgebaseerde oplossing. Deze oplossing brengt echter aanzienlijke I/O-kosten met zich mee. Volgende maand ga ik verder met het verkennen van aanvullende oplossingen.