Dit artikel gaat in op de schatting van selectiviteit en kardinaliteit voor predikaten op COUNT(*) uitdrukkingen, zoals te zien is in HAVING clausules. De details zijn hopelijk op zich interessant. Ze bieden ook inzicht in enkele van de algemene benaderingen en algoritmen die worden gebruikt door de kardinaliteitsschatter.
Een eenvoudig voorbeeld met behulp van de AdventureWorks-voorbeelddatabase:
SELECT A.City FROM Person.[Address] AS A GROUP BY A.City HAVING COUNT_BIG(*) = 1;
We zijn geïnteresseerd in hoe SQL Server een schatting afleidt voor het predikaat op de count-expressie in de HAVING clausule.
Natuurlijk de HAVING clausule is gewoon syntaxis suiker. We hadden de query evengoed kunnen schrijven met behulp van een afgeleide tabel, of een algemene tabel-expressie:
-- Derived table
SELECT SQ1.City
FROM
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
) AS SQ1
WHERE SQ1.Expr1001 = 1;
-- CTE
WITH Grouped AS
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
)
SELECT G.City
FROM Grouped AS G
WHERE G.Expr1001 = 1; Alle drie de queryformulieren produceren hetzelfde uitvoeringsplan, met identieke hash-waarden voor het queryplan.
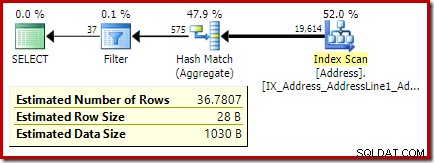
Het (werkelijke) plan na de uitvoering toont een perfecte schatting voor het totaal; echter, de schatting voor de HAVING clausulefilter (of equivalent, in de andere vraagformulieren) is slecht:
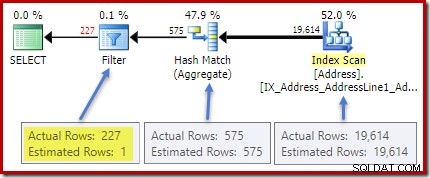
Statistieken over de City kolom nauwkeurige informatie geven over het aantal verschillende stadswaarden:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH DENSITY_VECTOR;
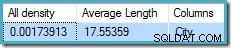
De alle dichtheid figuur is het omgekeerde van het aantal unieke waarden. Eenvoudig berekenen (1 / 0,00173913) =575 geeft de kardinaliteitsschatting voor het aggregaat. Groeperen op stad levert uiteraard één rij op voor elke afzonderlijke waarde.
Merk op dat alle dichtheid komt van de dichtheidsvector. Pas op dat u niet per ongeluk de dichtheid . gebruikt waarde uit de uitvoer van de statistiekkop van DBCC SHOW_STATISTICS . De kopdichtheid wordt alleen gehandhaafd voor achterwaartse compatibiliteit; het wordt tegenwoordig niet gebruikt door de optimizer tijdens de schatting van de kardinaliteit.
Het probleem
Het aggregaat introduceert een nieuwe berekende kolom in de workflow, genaamd Expr1001 in het uitvoeringsplan. Het bevat de waarde van COUNT(*) in elke gegroepeerde uitvoerrij:
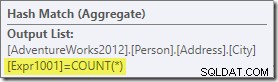
Er is duidelijk geen statistische informatie in de database over deze nieuwe berekende kolom. Hoewel de optimizer weet dat er 575 rijen zullen zijn, weet hij niets over de distributie aantal telwaarden binnen die rijen.
Nou, niet helemaal niets:de optimizer is zich ervan bewust dat de telwaarden positieve gehele getallen zullen zijn (1, 2, 3...). Toch is het de verdeling van deze gehele tellingswaarden over de 575 rijen die nodig zou zijn om de selectiviteit van de COUNT(*) = 1 nauwkeurig te schatten. predikaat.
Je zou kunnen denken dat een soort distributie-informatie zou kunnen worden afgeleid uit het histogram, maar het histogram geeft alleen specifieke telinformatie (in EQ_ROWS ) voor histogramstapwaarden. Tussen histogramstappen hebben we alleen een samenvatting:RANGE_ROWS rijen hebben DISTINCT_RANGE_ROWS onderscheiden waarden. Voor tabellen die groot genoeg zijn dat we ons zorgen maken over de kwaliteit van de selectiviteitsschatting, is het zeer waarschijnlijk dat het grootste deel van de tabel wordt weergegeven door deze intra-stapsamenvattingen.
Bijvoorbeeld, de eerste twee rijen van de City kolomhistogram zijn:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH HISTOGRAM;

Dit vertelt ons dat er precies één rij is voor "Abingdon", en 29 andere rijen na "Abingdon" maar vóór "Ballard", met 19 verschillende waarden in dat bereik van 29 rijen. De volgende query toont de werkelijke verdeling van rijen over unieke waarden in dat intra-stapbereik van 29 rijen:
SELECT A.City, NumRows = COUNT_BIG(*) FROM Person.[Address] AS A WHERE A.City > N'Abingdon' AND A.City < N'Ballard' GROUP BY ROLLUP (A.City);

Er zijn 29 rijen met 19 verschillende waarden, precies zoals het histogram zei. Toch is het duidelijk dat we geen basis hebben om de selectiviteit van een predikaat op de tellingkolom in die query te evalueren. Bijvoorbeeld, HAVING COUNT_BIG(*) = 2 zou 5 rijen teruggeven (voor Alexandria, Altadena, Atlanta, Augsburg en Austin), maar we kunnen dat op geen enkele manier bepalen uit het histogram.
Een goed opgeleide gok
De benadering van SQL Server is om aan te nemen dat elke groep meest waarschijnlijk . is om het totale gemiddelde (gemiddelde) aantal rijen te bevatten. Dit is gewoon de kardinaliteit gedeeld door het aantal unieke waarden. Voor 1000 rijen met 20 unieke waarden zou SQL Server bijvoorbeeld aannemen dat (1000/20) =50 rijen per groep de meest waarschijnlijke waarde is.
Terugkerend naar ons oorspronkelijke voorbeeld, betekent dit dat de berekende tellingskolom "meest waarschijnlijk" een waarde bevat rond (1914/575) ~=34.1113 . Sinds dichtheid het omgekeerde is van het aantal unieke waarden, kunnen we dat ook uitdrukken als kardinaliteit * dichtheid =(1914 * 0,00173913), wat een zeer vergelijkbaar resultaat geeft.
Distributie
Zeggen dat de gemiddelde waarde hoogstwaarschijnlijk alleen is, brengt ons zo ver. We moeten ook vaststellen hoe waarschijnlijk dat precies is; en hoe de waarschijnlijkheid verandert als we van de gemiddelde waarde af gaan. Ervan uitgaande dat alle groepen in ons voorbeeld precies 34.113 rijen hebben, zou geen erg "opgeleide" gok zijn!
SQL Server handelt dit af door uit te gaan van een normale verdeling. Dit heeft de karakteristieke klokvorm die je misschien al kent (afbeelding uit het gelinkte Wikipedia-item):
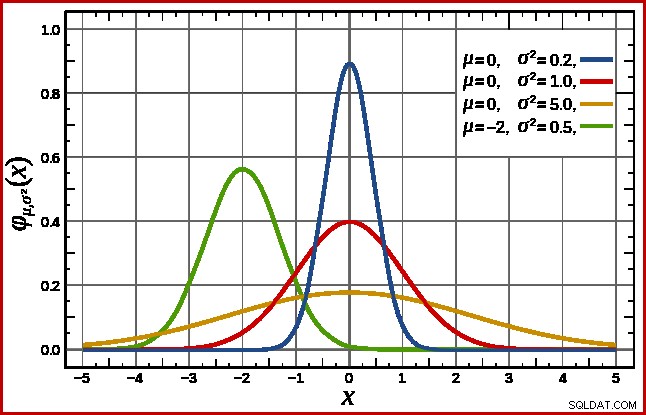
De exacte vorm van de normale verdeling hangt af van twee parameters :het gemiddelde (µ ) en de standaarddeviatie (σ ). Het gemiddelde bepaalt de locatie van de piek. De standaarddeviatie geeft aan hoe "afgeplat" de belcurve is. Hoe vlakker de curve, hoe lager de piek en hoe meer de kansdichtheid wordt verdeeld over andere waarden.
SQL Server kan het gemiddelde afleiden uit statistische informatie, zoals reeds opgemerkt. De standaarddeviatie van de berekende telkolomwaarden is onbekend. SQL Server schat het als de vierkantswortel van het gemiddelde (met een kleine aanpassing die later gedetailleerd wordt). In ons voorbeeld betekent dit dat de twee parameters van de normale verdeling ruwweg 34.1113 en 5.84 (de vierkantswortel) zijn.
De standaard normale verdeling (de rode curve in het diagram hierboven) is een opmerkelijk speciaal geval. Dit gebeurt wanneer het gemiddelde nul is en de standaarddeviatie 1 is. Elke normale verdeling kan worden omgezet in de standaardnormale verdeling door het gemiddelde af te trekken en te delen door de standaarddeviatie.
Gebieden en intervallen
We zijn geïnteresseerd in het schatten van selectiviteit, dus we zoeken naar de kans dat de berekende kolom een bepaalde waarde (x) heeft. Deze kans wordt niet gegeven door de waarde van de y-as hierboven, maar door het gebied onder de curve links van x.
Voor de normale verdeling met gemiddelde 34,1113 en standaarddeviatie 5,84 is het gebied onder de curve links van x =30 ongeveer 0,2406:
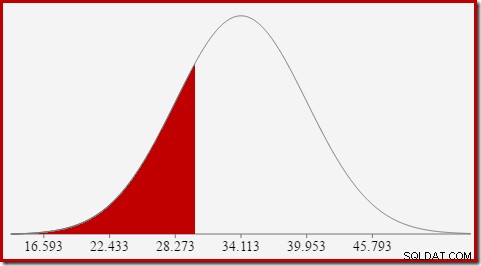
Dit komt overeen met de kans dat de kolom voor het berekende aantal kleiner dan of gelijk is aan 30 voor onze voorbeeldquery.
Dit leidt mooi naar het idee dat we in het algemeen niet op zoek zijn naar de kans op een bepaalde waarde, maar naar een interval . Om de waarschijnlijkheid te vinden dat het aantal gelijk is aan een geheel getal is, moeten we er rekening mee houden dat gehele getallen een interval van grootte 1 overspannen. Hoe we een geheel getal naar een interval converteren, is enigszins willekeurig. SQL Server handelt dit af door 0,5 . op te tellen en af te trekken om de onder- en bovengrenzen van het interval te geven.
Om bijvoorbeeld de kans te vinden dat de berekende telwaarde gelijk is aan 30, moeten we aftrekken het gebied onder de normale verdelingscurve voor (x =29,5) van het gebied voor (x =30,5). Het resultaat komt overeen met het segment voor (29,5
De oppervlakte van de rode schijf is ongeveer 0,0533 . Voor een goede eerste benadering is dit de selectiviteit van een predikaat count =30 in onze testquery.
Het berekenen van de oppervlakte onder een normale verdeling links van een gegeven waarde is niet eenvoudig. De algemene formule wordt gegeven door de cumulatieve verdelingsfunctie (CDF). Het probleem is dat de CDF niet kan worden uitgedrukt in termen van elementaire wiskundige functies, dus in plaats daarvan moeten numerieke benaderingsmethoden worden gebruikt.
Aangezien alle normale verdelingen gemakkelijk kunnen worden getransformeerd naar de standaard normale verdeling (gemiddelde =0, standaarddeviatie =1), werken de benaderingen allemaal om de standaardnormaal te schatten. Dit betekent dat we moeten transformeren onze intervalgrenzen van de specifieke normale verdeling die past bij de zoekopdracht, tot de standaard normale verdeling. Dit wordt gedaan, zoals eerder vermeld, door het gemiddelde af te trekken en te delen door de standaarddeviatie.
Als u bekend bent met Excel, kent u wellicht de functies NORM.DIST en NORM.S.DIST die CDF's kunnen berekenen (met behulp van numerieke benaderingsmethoden) voor een bepaalde normale verdeling of de standaard normale verdeling.
Er is geen CDF-calculator ingebouwd in SQL Server, maar we kunnen er gemakkelijk een maken. Aangezien de CDF voor de standaard normale verdeling is:
...waar erf is de foutfunctie:
Hieronder wordt een T-SQL-implementatie weergegeven om de CDF voor de standaard normale verdeling te verkrijgen. Het gebruikt een numerieke benadering voor de foutfunctie dat heel dicht bij wat SQL Server intern gebruikt:
Een voorbeeld om de CDF voor x =30 te berekenen met behulp van de normale verdeling voor onze testquery:
Let op de normalisatiestap om te converteren naar de standaard normale verdeling. De procedure retourneert de waarde 0.2407196…, die overeenkomt met het corresponderende Excel-resultaat tot op zeven decimalen.
De volgende code past onze voorbeeldquery aan om een grotere schatting voor het filter te produceren (de vergelijking is nu met de waarde 32, wat veel dichter bij het gemiddelde ligt dan voorheen):
De schatting van de optimizer is nu 36,7807 .
Om de schatting handmatig te berekenen, moeten we eerst een paar laatste details behandelen:
De volgende procedure bevat alle details in dit artikel. Het vereist de eerder gegeven CDF-procedure:
We kunnen nu deze procedure gebruiken om een schatting te maken voor onze nieuwe testquery:
De uitvoer is:
Dit komt heel goed overeen met de kardinaliteitsschatting van de optimizer van 36,7807.
De procedure kan worden gebruikt voor andere telintervallen naast gelijkheidstesten. Het enige dat nodig is, is het instellen van de
Om dit met onze procedure te gebruiken, stellen we
Het resultaat is 572.5964:
Een laatste voorbeeld met
De optimalisatieschatting is
Sinds
Nogmaals, dit komt overeen met de schatting van de optimalisatie.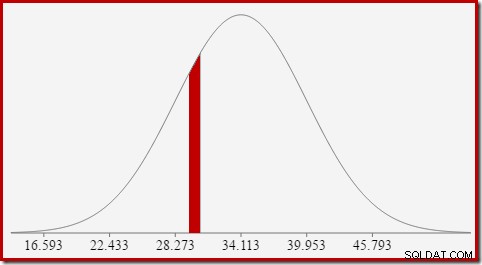
De cumulatieve distributiefunctie
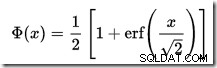
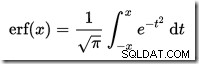
CREATE PROCEDURE dbo.GetStandardNormalCDF
(
@x float,
@cdf float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
DECLARE
@sign float,
@erf float;
SET @sign = SIGN(@x);
SET @x = ABS(@x) / SQRT(2);
SET @erf = 1;
SET @erf = @erf + (0.0705230784 * @x);
SET @erf = @erf + (0.0422820123 * POWER(@x, 2));
SET @erf = @erf + (0.0092705272 * POWER(@x, 3));
SET @erf = @erf + (0.0001520143 * POWER(@x, 4));
SET @erf = @erf + (0.0002765672 * POWER(@x, 5));
SET @erf = @erf + (0.0000430638 * POWER(@x, 6));
SET @erf = POWER(@erf, -16);
SET @erf = 1 - @erf;
SET @erf = @erf * @sign;
SET @cdf = 0.5 * (1 + @erf);
END; DECLARE @cdf float;
DECLARE @x float;
-- HAVING COUNT_BIG(*) = x
SET @x = 30;
-- Normalize 30 by subtracting the mean
-- and dividing by the standard deviation
SET @x = (@x - 34.1113) / 5.84;
EXECUTE dbo.GetStandardNormalCDF
@x = @x,
@cdf = @cdf OUTPUT;
SELECT CDF = @cdf; Laatste details en voorbeelden
SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) = 32;
COUNT(*) = 1 , die hier niet wordt beschreven. COUNT(*) = 1 In het geval dat de oude CE dezelfde logica gebruikt als de nieuwe CE (beschikbaar vanaf SQL Server 2014).CREATE PROCEDURE dbo.GetCountPredicateEstimate
(
@From integer,
@To integer,
@Cardinality float,
@Density float,
@Selectivity float OUTPUT,
@Estimate float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
BEGIN TRY
DECLARE
@Start float,
@End float,
@Distinct float,
@Mean float,
@MeanAdj float,
@Stdev float,
@NormStart float,
@NormEnd float,
@CDFStart float,
@CDFEnd float;
-- Validate input and apply defaults
IF ISNULL(@From, 0) = 0 SET @From = 1;
IF @From < 1 RAISERROR ('@From must be >= 1', 16, 1);
IF ISNULL(@Cardinality, -1) <= 0 RAISERROR('@Cardinality must be positive', 16, 1);
IF ISNULL(@Density, -1) <= 0 RAISERROR('@Density must be positive', 16, 1);
IF ISNULL(@To, 0) = 0 SET @To = CEILING(1 / @Density);
IF @To < @From RAISERROR('@To must be >= @From', 16, 1);
-- Convert integer range to interval
SET @Start = @From - 0.5;
SET @End = @To + 0.5;
-- Get number of distinct values
SET @Distinct = 1 / @Density;
-- Calculate mean
SET @Mean = @Cardinality * @Density;
-- Adjust mean;
SET @MeanAdj = @Mean * ((@Distinct - 1) / @Distinct);
-- Get standard deviation (guess)
SET @Stdev = SQRT(@MeanAdj);
-- Normalize interval
SET @NormStart = (@Start - @Mean) / @Stdev;
SET @NormEnd = (@End - @Mean) / @Stdev;
-- Calculate CDFs
EXECUTE dbo.GetStandardNormalCDF
@x = @NormStart,
@cdf = @CDFStart OUTPUT;
EXECUTE dbo.GetStandardNormalCDF
@x = @NormEnd,
@cdf = @CDFEnd OUTPUT;
-- Selectivity
SET @Selectivity =
CASE
-- Unbounded start
WHEN @From = 1 THEN @CDFEnd
-- Unbounded end
WHEN @To >= @Distinct THEN 1 - @CDFStart
-- Normal interval
ELSE @CDFEnd - @CDFStart
END;
-- Return row estimate
SET @Estimate = @Selectivity * @Distinct;
END TRY
BEGIN CATCH
DECLARE @EM nvarchar(4000) = ERROR_MESSAGE();
IF @@TRANCOUNT > 0 ROLLBACK TRANSACTION;
RAISERROR (@EM, 16, 1);
RETURN;
END CATCH;
END; DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = 32,
@To = 32,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
Voorbeelden van ongelijkheidsinterval
@From en @To parameters naar de integer-intervalgrenzen. Om onbegrensd op te geven, geef je nul of NULL . door zoals je wilt.SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) < 50;

@From = NULL . in en @To = 49 (omdat 50 wordt uitgesloten door minder dan):DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = NULL,
@To = 49,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
BETWEEN :SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) BETWEEN 25 AND 30;

BETWEEN is inclusief, we passeren de procedure @From = 25 en @To = 30 . Het resultaat is:
