Uitdagingsoplossingen voor generatorreeksen voor getallen - Deel 5

Dit is het vijfde en laatste deel in de serie over oplossingen voor de uitdaging van de nummerreeksgenerator. In deel 1, deel 2, deel 3 en deel 4 heb ik pure T-SQL-oplossingen behandeld. Toen ik de puzzel al vroeg postte, merkten verschillende mensen op dat de best presterende oplossing waarschijnlijk een op CLR gebaseerde oplossing zou zijn. In dit artikel zullen we deze intuïtieve veronderstelling op de proef stellen. In het bijzonder zal ik op CLR gebaseerde oplossingen behandelen die zijn gepost door Kamil Kosno en Adam Machanic.

Veel dank aan Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea en Paul White voor het delen van uw ideeën en opmerkingen.

Ik doe mijn testen in een database genaamd testdb. Gebruik de volgende code om de database te maken als deze niet bestaat, en om I/O- en tijdstatistieken in te schakelen:

-- DB en statsSET NOCOUNT ON;SET STATISTICS IO, TIME ON;GO IF DB_ID('testdb') IS NULL MAAK DATABASE testdb;GO GEBRUIK testdb;GO

Voor de eenvoud zal ik de strikte beveiliging van CLR uitschakelen en de database betrouwbaar maken met behulp van de volgende code:

-- Schakel CLR in, schakel CLR strikte beveiliging uit en maak db betrouwbaarEXEC sys.sp_configure 'toon geavanceerde instellingen', 1;RECONFIGURE; EXEC sys.sp_configure 'clr ingeschakeld', 1;EXEC sys.sp_configure 'clr strikte beveiliging', 0;HERCONFIGUREREN; EXEC sys.sp_configure 'toon geavanceerde instellingen', 0;HERCONFIGUREREN; WIJZIG DATABASE testdb STEL BETROUWBAAR IN; GO

Eerdere oplossingen

Voordat ik inga op de op CLR gebaseerde oplossingen, laten we even de prestaties bekijken van twee van de best presterende T-SQL-oplossingen.

De best presterende T-SQL-oplossing die geen persistente basistabellen gebruikte (behalve de dummy lege columnstore-tabel om batchverwerking te krijgen), en daarom geen I/O-bewerkingen behelsde, was degene die werd geïmplementeerd in de functie dbo.GetNumsAlanCharlieItzikBatch. Ik heb deze oplossing behandeld in deel 1.

Hier is de code om de dummy lege columnstore-tabel te maken die de query van de functie gebruikt:

TABEL VERLATEN INDIEN BESTAAT dbo.BatchMe;GO MAAK TABEL dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);GO

En hier is de code met de functiedefinitie:

FUNCTIE MAKEN OF WIJZIGEN dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT =1, @high AS BIGINT) RETURN TABLEASRETURN MET L0 AS ( SELECTEER 1 ALS c UIT (VALUES(1),(1),(1),(1 ),(1),(1),(1),(1), (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c)), L1 AS ( SELECTEER 1 ALS c VAN L0 ALS EEN KRUISVORM VAN L0 ALS B ), L2 AS ( SELECTEER 1 ALS c VAN L1 ALS EEN KRUISVERBINDING VAN L1 ALS B ), L3 AS ( SELECTEER 1 ALS c VAN L2 ALS EEN CROSS JOIN L2 AS B), Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum VAN L3 ) SELECT TOP(@high - @low + 1) rownum AS rn, @high + 1 - rownum AS op, @low - 1 + rownum AS n VAN Nums LEFT OUTER JOIN dbo.BatchMe ON 1 =0 ORDER BY rownum;GO

Laten we eerst de functie testen die een reeks van 100 miljoen getallen aanvraagt, met het MAX-aggregaat toegepast op kolom n:

SELECTEER MAX(n) AS mx VAN dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTIE(MAXDOP 1);

Bedenk dat deze testtechniek het verzenden van 100 miljoen rijen naar de beller vermijdt, en ook de inspanning in de rijmodus die gepaard gaat met variabele toewijzing bij gebruik van de variabele toewijzingstechniek.

Dit zijn de tijdstatistieken die ik voor deze test op mijn computer heb gekregen:

De uitvoering van deze functie levert natuurlijk geen logische reads op.

Laten we het vervolgens met volgorde testen, met behulp van de variabele toewijzingstechniek:

VERKLAREN @n ALS GROOT; SELECT @n =n VAN dbo.GetNumsAlanCharlieItzikBatch (1, 100000000) BESTELLEN DOOR n OPTIE (MAXDOP 1);

Ik heb de volgende tijdstatistieken voor deze uitvoering:

Bedenk dat deze functie niet resulteert in sorteren bij het opvragen van de gegevens die zijn geordend op n; u krijgt in principe hetzelfde abonnement, of u nu de bestelde gegevens opvraagt ​​of niet. We kunnen de meeste extra tijd in deze test in vergelijking met de vorige toeschrijven aan de 100 miljoen rij-modus gebaseerde variabele toewijzingen.

De best presterende T-SQL-oplossing die gebruikmaakte van een persistente basistabel en daarom resulteerde in een aantal I/O-bewerkingen, hoewel zeer weinig, was de oplossing van Paul White, geïmplementeerd in de functie dbo.GetNums_SQLkiwi. Ik heb deze oplossing in deel 4 behandeld.

Hier is de code van Paul om zowel de columnstore-tabel te maken die door de functie als de functie zelf wordt gebruikt:

-- Helper columnstore tableDROP TABLE INDIEN BESTAAT dbo.CS; -- 64K rijen (genoeg voor 4B rijen wanneer kruiselings samengevoegd) -- kolom 1 is altijd nul -- kolom 2 is (1...65536) SELECT -- typ als geheel getal NOT NULL -- (alles is genormaliseerd naar 64 bits in columnstore/batch-modus sowieso) n1 =ISNULL(CONVERT(integer, 0), 0), n2 =ISNULL(CONVERT(integer, N.rn), 0)INTO dbo.CSFROM ( SELECT rn =ROW_NUMBER() OVER (ORDER BY @@SPID) VAN master.dbo.spt_values ​​AS SV1 CROSS JOIN master.dbo.spt_values ​​AS SV2 ORDER DOOR rn ASC OFFSET 0 RIJEN FETCH ALLEEN VOLGENDE 65536 RIJEN) ALS N; -- Enkele gecomprimeerde rijgroep van 65.536 rijen MAAK CLUSTERED COLUMNSTORE INDEX CCI OP dbo.CS WITH (MAXDOP =1);GO -- De functieCREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi( @low bigint =1, @high bigint)RETURNS table ASRETURN SELECT N .rn, n =@low - 1 + N.rn, op =@high + 1 - N.rn FROM ( SELECT -- Gebruik @@TRANCOUNT in plaats van @@SPID als je al je vragen wilt hebben serial rn =ROW_NUMBER() OVER (ORDER DOOR @@SPID ASC) VANAF dbo.CS AS N1 JOIN dbo.CS AS N2 -- Batch-modus hash cross join -- Integer niet null gegevenstype vermijd hash-sonde resterend -- Dit is altijd 0 =0 OP N2. n1 =N1.n1 WHERE -- Probeer SQRT op negatieve getallen te vermijden en vereenvoudiging mogelijk te maken -- naar een enkele constante scan als @low> @high (met letterlijke waarden) -- Geen opstartfilters in batchmodus @high>=@low -- Grof filter:-- Beperk elke kant van de cross join naar SQRT(doelaantal rijen) -- IIF vermijdt SQRT op negatieve getallen met parameters AND N1.n2 <=CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high>=@low, @high) - @laag + 1, 0))))) AND N2.n2 <=CONVERT(integer, PLAFOND(SQRT(CONVERT(float, IIF(@high>=@low, @high - @low + 1, 0)) ))) ) AS N WHERE -- Nauwkeurig filter:-- Batch-modus filter de beperkte cross-join tot het exacte aantal rijen dat nodig is -- Vermijdt dat de optimizer een rij-modus Top introduceert met de volgende row-modus compute scalar @low - 2 + N.rn <@high;GO

Laten we het eerst zonder bestelling testen met behulp van de aggregatietechniek, wat resulteert in een all-batch-mode-plan:

SELECTEER MAX(n) AS mx VANAF dbo.GetNums_SQLkiwi(1, 100000000) OPTIE(MAXDOP 1);

Ik heb de volgende tijd- en I/O-statistieken voor deze uitvoering:

Laten we de functie met volgorde testen met behulp van de variabele toewijzingstechniek:

VERKLAREN @n ALS GROOT; SELECT @n =n FROM dbo.GetNums_SQLkiwi (1, 100000000) BESTELLEN DOOR n OPTIE (MAXDOP 1);

Net als bij de vorige oplossing, vermijdt deze oplossing expliciete sortering in het plan, en krijgt daarom hetzelfde plan, of u nu om de bestelde gegevens vraagt ​​of niet. Maar nogmaals, deze test levert een extra boete op, voornamelijk vanwege de variabele toewijzingstechniek die hier wordt gebruikt, waardoor het variabele toewijzingsgedeelte in het plan in rijmodus wordt verwerkt.

Dit zijn de tijd- en I/O-statistieken die ik voor deze uitvoering heb gekregen:

CLR-oplossingen

Zowel Kamil Kosno als Adam Machanic leverden eerst een eenvoudige CLR-only oplossing en kwamen later met een meer geavanceerde CLR+T-SQL-combo. Ik zal beginnen met de oplossingen van Kamil en daarna de oplossingen van Adam bespreken.

Oplossingen door Kamil Kosno

Hier is de CLR-code die in de eerste oplossing van Kamil wordt gebruikt om een ​​functie met de naam GetNums_KamilKosno1 te definiëren:

gebruikend System;gebruikend System.Data.SqlTypes;gebruikend System.Collections;openbare gedeeltelijke klasse GetNumsKamil1{ [Microsoft.SqlServer.Server.SqlFunction(FillRowMethodName ="GetNums_KamilKosno1_Fill", TableDefinition_Numator ="n BIGINT") (SqlInt64 laag, SqlInt64 hoog) {return (low.IsNull || high.IsNull) ? nieuwe GetNumsCS(0, 0) :nieuwe GetNumsCS(lage.Waarde, hoge.Waarde); } public static void GetNums_KamilKosno1_Fill(Object o, out SqlInt64 n) { n =(long)o; } privéklasse GetNumsCS:IEnumerator { public GetNumsCS (lang van, lang naar) { _lowrange =van; _current =_laag bereik - 1; _hoog bereik =naar; } public bool MoveNext() { _current +=1; if (_current> _highrange) retourneer false; anders retour waar; } publiek object Current { get { return _current; } } public void Reset() { _current =_lowrange - 1; } lang _laag bereik; lange _stroom; lang _hoog bereik; }}

De functie accepteert twee invoer genaamd laag en hoog en retourneert een tabel met een BIGINT-kolom genaamd n. De functie is een streaming-soort, die een rij retourneert met het volgende nummer in de reeks per rijverzoek van de aanroepende query. Zoals je kunt zien, koos Kamil voor de meer geformaliseerde methode voor het implementeren van de IEnumerator-interface, waarbij de methoden MoveNext worden geïmplementeerd (de enumerator wordt naar voren gehaald om de volgende rij te krijgen), Current (haalt de rij in de huidige enumeratorpositie) en Reset (sets de teller naar de beginpositie, die voor de eerste rij staat).

De variabele die het huidige nummer in de reeks bevat, wordt _current genoemd. De constructor stelt _current in op de ondergrens van het gevraagde bereik min 1, en hetzelfde geldt voor de Reset-methode. De MoveNext-methode verhoogt _current met 1. Als _current groter is dan de bovengrens van het gevraagde bereik, retourneert de methode false, wat betekent dat deze niet opnieuw wordt aangeroepen. Anders retourneert het waar, wat betekent dat het opnieuw wordt aangeroepen. De methode Current retourneert natuurlijk _current. Zoals je kunt zien, vrij eenvoudige logica.

Ik noemde het Visual Studio-project GetNumsKamil1 en gebruikte het pad C:\Temp\ ervoor. Dit is de code die ik heb gebruikt om de functie in de testdb-database te implementeren:

DROP-FUNCTIE INDIEN BESTAAT dbo.GetNums_KamilKosno1; DROP MONTAGE INDIEN BESTAAT GetNumsKamil1;GA MONTAGE MAKEN GetNumsKamil1 FROM 'C:\Temp\GetNumsKamil1\GetNumsKamil1\bin\Debug\GetNumsKamil1.dll';GO CREATE FUNCTION dbo_. TABLE(n BIGINT) ORDER(n) ALS EXTERNE NAAM GetNumsKamil1.GetNumsKamil1.GetNums_KamilKosno1;GO

Let op het gebruik van de ORDER-component in de CREATE FUNCTION-instructie. De functie zendt de rijen in n volgorde uit, dus wanneer de rijen in het plan in n volgorde moeten worden opgenomen, weet SQL Server op basis van deze clausule dat het een sortering in het plan kan vermijden.

Laten we de functie testen, eerst met de aggregaattechniek, wanneer bestellen niet nodig is:

SELECTEER MAX(n) AS mx VAN dbo.GetNums_KamilKosno1(1, 100000000);

Ik heb het plan weergegeven in figuur 1.

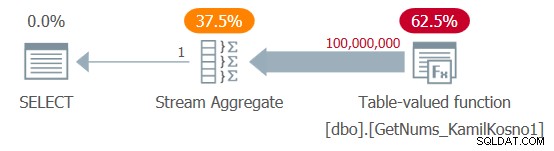Figuur 1:Plan voor de functie dbo.GetNums_KamilKosno1

Er valt niet veel te zeggen over dit plan, behalve dat alle operators de rij-uitvoeringsmodus gebruiken.

Ik heb de volgende tijdstatistieken voor deze uitvoering:

En natuurlijk waren er geen logische lezingen bij betrokken.

Laten we de functie testen met volgorde, met behulp van de variabele toewijzingstechniek:

VERKLAREN @n ALS GROOT; SELECT @n =n VAN dbo.GetNums_KamilKosno1(1, 100000000) BESTELLEN DOOR n;

Ik heb het plan weergegeven in figuur 2 voor deze uitvoering.

Figuur 2:Plan voor de functie dbo.GetNums_KamilKosno1 met ORDER BY

Merk op dat er niet wordt gesorteerd in het plan, aangezien de functie is gemaakt met de ORDER(n)-clausule. Er is echter enige inspanning nodig om ervoor te zorgen dat de rijen inderdaad in de beloofde volgorde door de functie worden uitgezonden. Dit wordt gedaan met behulp van de operators Segment en Sequence Project, die worden gebruikt om rijnummers te berekenen, en de operator Assert, die de uitvoering van de query afbreekt als de test mislukt. Dit werk heeft lineaire schaling - in tegenstelling tot de n log n schaling die je zou hebben gekregen als een sortering vereist was - maar het is nog steeds niet goedkoop. Ik heb de volgende tijdstatistieken voor deze test:

De resultaten zouden voor sommigen verrassend kunnen zijn, vooral degenen die intuïtief aannamen dat de op CLR gebaseerde oplossingen beter zouden presteren dan de T-SQL-oplossingen. Zoals u kunt zien, zijn de uitvoeringstijden een orde van grootte langer dan bij onze best presterende T-SQL-oplossing.

De tweede oplossing van Kamil is een CLR-T-SQL-hybride. Naast de lage en hoge invoer voegt de CLR-functie (GetNums_KamilKosno2) een stapinvoer toe en retourneert waarden tussen laag en hoog die een stap uit elkaar liggen. Hier is de CLR-code die Kamil in zijn tweede oplossing gebruikte:

systeem gebruiken; System.Data.SqlTypes gebruiken; System.Collections gebruiken; openbare gedeeltelijke klasse GetNumsKamil2{ [Microsoft.SqlServer.Server.SqlFunction(DataAccess =Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic =true, IsPrecise =true, FillRowMethodName ="GetNumfin_Fill ="", B IEnumerator GetNums_KamilKosno2 (SqlInt64 laag, SqlInt64 hoog, SqlInt64 stap) { return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) :nieuw GetNumsCS(low.Value, high.Value, step.Value); } public static void GetNums_Fill(Object o, out SqlInt64 n) { n =(long)o; } privéklasse GetNumsCS:IEnumerator { public GetNumsCS (lang van, lang naar, lange stap) { _lowrange =van; _stap =stap; _current =_lowrange - _step; _hoog bereik =naar; } public bool MoveNext() { _current =_current + _step; if (_current> _highrange) retourneert false; anders retour waar; } publiek object Current { get { return _current; } } public void Reset() { _current =_lowrange - _step; } lang _laag bereik; lange _stroom; lang _hoog bereik; lange _stap; }}

Ik noemde het VS-project GetNumsKamil2, plaatste het ook in het pad C:\Temp\ en gebruikte de volgende code om het in de testdb-database te implementeren:

Als voorbeeld voor het gebruik van de functie is hier een verzoek om waarden tussen 5 en 59 te genereren, met een stap van 10:

SELECTEER n VAN dbo.GetNums_KamilKosno2(5, 59, 10);

Deze code genereert de volgende uitvoer:

n---51525354555

Wat het T-SQL-gedeelte betreft, gebruikte Kamil een functie genaamd dbo.GetNums_Hybrid_Kamil2, met de volgende code:

FUNCTIE MAKEN OF WIJZIGEN dbo.GetNums_Hybrid_Kamil2(@low AS BIGINT, @high AS BIGINT) RETURNS TABLEASRETURN SELECT TOP (@high - @low + 1) V.n VAN dbo.GetNums_KamilKosno2(@low, @high, 10) ALS GN KRUIS TOEPASSEN (WAARDEN(0+GN.n),(1+GN.n),(2+GN.n),(3+GN.n),(4+GN.n), (5+GN.n ),(6+GN.n),(7+GN.n),(8+GN.n),(9+GN.n)) AS V(n);GO

Zoals u kunt zien, roept de T-SQL-functie de CLR-functie aan met dezelfde @low- en @high-invoer die deze krijgt, en in dit voorbeeld wordt een stapgrootte van 10 gebruikt. De query gebruikt CROSS APPLY tussen het resultaat van de CLR-functie en een table -value constructor die de laatste getallen genereert door waarden in het bereik van 0 tot en met 9 toe te voegen aan het begin van de stap. Het TOP-filter wordt gebruikt om ervoor te zorgen dat je niet meer krijgt dan het aantal nummers dat je hebt aangevraagd.

Belangrijk: Ik moet benadrukken dat Kamil hier een aanname doet dat het TOP-filter wordt toegepast op basis van de volgorde van het resultaatnummer, wat niet echt gegarandeerd is omdat de zoekopdracht geen ORDER BY-clausule heeft. Als u ofwel een ORDER BY-component toevoegt om TOP te ondersteunen, of TOP vervangt door een WHERE-filter, om een ​​deterministisch filter te garanderen, kan dit het prestatieprofiel van de oplossing volledig veranderen.

Laten we in ieder geval eerst de functie zonder volgorde testen met behulp van de aggregatietechniek:

SELECTEER MAX(n) AS mx FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000);

Ik heb het plan weergegeven in figuur 3 voor deze uitvoering.

Figuur 3:Plan voor de functie dbo.GetNums_Hybrid_Kamil2

Nogmaals, alle operators in het plan gebruiken rij-uitvoeringsmodus.

Ik heb de volgende tijdstatistieken voor deze uitvoering:

En natuurlijk geen logische leest.

Laten we de functie testen met volgorde:

VERKLAREN @n ALS GROOT; SELECT @n =n VAN dbo.GetNums_Hybrid_Kamil2(1, 100000000) BESTELLEN DOOR n;

Ik heb het plan weergegeven in figuur 4.

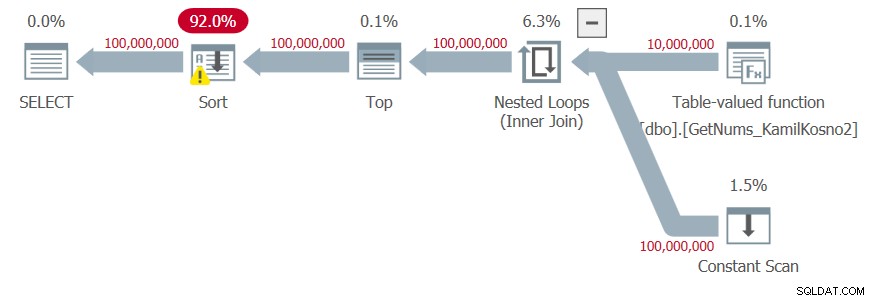Figuur 4:Plan voor dbo.GetNums_Hybrid_Kamil2 functie met ORDER BY

Aangezien de resultaatgetallen het resultaat zijn van manipulatie van de ondergrens van de stap die wordt geretourneerd door de CLR-functie en de delta die is toegevoegd in de tabelwaarde-constructor, vertrouwt de optimizer er niet op dat de resultaatgetallen in de gevraagde volgorde worden gegenereerd, en voegt expliciete sortering toe aan het plan.

Ik heb de volgende tijdstatistieken voor deze uitvoering:

Het lijkt er dus op dat wanneer er geen bestelling nodig is, de tweede oplossing van Kamil het beter doet dan zijn eerste. Maar als er orde nodig is, is het andersom. Hoe dan ook, de T-SQL-oplossingen zijn sneller. Persoonlijk zou ik de juistheid van de eerste oplossing vertrouwen, maar niet de tweede.

Oplossingen door Adam Machanic

Adams eerste oplossing is ook een basis CLR-functie die een teller blijft verhogen. Alleen in plaats van de meer ingewikkelde, geformaliseerde aanpak te gebruiken zoals Kamil deed, gebruikte Adam een ​​eenvoudigere aanpak die het opbrengstcommando per rij oproept dat moet worden geretourneerd.

Hier is Adams CLR-code voor zijn eerste oplossing, die een streamingfunctie definieert met de naam GetNums_AdamMachanic1:

System.Data.SqlTypes gebruiken;System.Collections gebruiken; openbare gedeeltelijke klasse GetNumsAdam1{ [Microsoft.SqlServer.Server.SqlFunction( FillRowMethodName ="GetNums_AdamMachanic1_fill", TableDefinition ="n BIGINT")] openbare statische IEnumerable GetNums_AdamMachanic1(SqlInt64 min.64, SqlInt64 min_max;) var max_int =max.Waarde; for (; min_int <=max_int; min_int++) {opbrengstrendement (min_int); } } public static void GetNums_AdamMachanic1_fill(object o, out long i) { i =(long)o; }};

De oplossing is zo elegant in zijn eenvoud. Zoals u kunt zien, accepteert de functie twee invoer genaamd min en max die de lage en hoge grenspunten van het gevraagde bereik vertegenwoordigen, en retourneert een tabel met een BIGINT-kolom met de naam n. De functie initialiseert variabelen genaamd min_int en max_int met de invoerparameterwaarden van de respectieve functie. De functie voert vervolgens een lus uit zo lang als min_int <=max_int, die in elke iteratie een rij oplevert met de huidige waarde van min_int en min_int met 1 verhoogt. Dat is alles.

Ik noemde het project GetNumsAdam1 in VS, plaatste het in C:\Temp\ en gebruikte de volgende code om het te implementeren:

-- Creëer assembly en functieDROP FUNCTIE INDIEN BESTAAT dbo.GetNums_AdamMachanic1;DROP ASSEMBLY INDIEN BESTAAT GetNumsAdam1;GO MAAK ASSEMBLY GetNumsAdam1 FROM 'C:\Temp\GetNumsAdam1\GetNumsAREATED .GetNums_AdamMachanic1(@low AS BIGINT =1, @high AS BIGINT) RETOURTABEL(n BIGINT) ORDER(n) ALS EXTERNE NAAM GetNumsAdam1.GetNumsAdam1.GetNums_AdamMachanic1;GO

Ik heb de volgende code gebruikt om het te testen met de aggregatietechniek, voor gevallen waarin volgorde er niet toe doet:

SELECTEER MAX(n) AS mx FROM dbo.GetNums_AdamMachanic1(1, 100000000);

Ik heb het plan weergegeven in figuur 5 voor deze uitvoering.

Figuur 5:Plan voor de functie dbo.GetNums_AdamMachanic1

Het plan lijkt erg op het plan dat u eerder zag voor de eerste oplossing van Kamil, en hetzelfde geldt voor de prestaties. Ik heb de volgende tijdstatistieken voor deze uitvoering:

En natuurlijk waren er geen logische reads nodig.

Laten we de functie testen met volgorde, met behulp van de variabele toewijzingstechniek:

VERKLAREN @n ALS GROOT; SELECT @n =n VAN dbo.GetNums_AdamMachanic1(1, 100000000) BESTELLEN DOOR n;

Ik heb het plan weergegeven in figuur 6 voor deze uitvoering.

Figuur 6:Plan voor dbo.GetNums_AdamMachanic1 functie met ORDER BY

Nogmaals, het plan lijkt op het plan dat je eerder zag voor de eerste oplossing van Kamil. Er was geen behoefte aan expliciete sortering omdat de functie is gemaakt met de ORDER-clausule, maar het plan omvat wel wat werk om te verifiëren dat de rijen inderdaad worden geretourneerd, in volgorde zoals beloofd.

Ik heb de volgende tijdstatistieken voor deze uitvoering:

In zijn tweede oplossing combineerde Adam ook een CLR-deel en een T-SQL-deel. Hier is Adams beschrijving van de logica die hij in zijn oplossing gebruikte:

CLR is een goed antwoord voor het tweede deel, maar wordt natuurlijk gehinderd door het eerste nummer. Dus als compromis heb ik een T-SQL TVF gemaakt [genaamd GetNums_AdamMachanic2_8192] hardcoded met de waarden 1 tot en met 8192. (Vrij arbitraire keuze, maar te groot en de QO begint er een beetje in te stikken.) Vervolgens wijzigde ik mijn CLR-functie [ met de naam GetNums_AdamMachanic2_8192_base] om twee kolommen uit te voeren, "max_base" en "base_add", en liet het rijen uitvoeren zoals:

max_base, base_add
—————
8191, 1
8192, 8192
8192, 16384
…
8192, 99991552
257, 99999744

Nu is het een simpele lus. De CLR-uitvoer wordt verzonden naar de T-SQL TVF, die is ingesteld om alleen maximaal "max_base" rijen van de hardcoded set terug te sturen. En voor elke rij voegt het "base_add" toe aan de waarde, waardoor de vereiste getallen worden gegenereerd. De sleutel hier is, denk ik, dat we N rijen kunnen genereren met slechts een enkele logische kruisverbinding, en de CLR-functie hoeft maar 1/8192 zoveel rijen terug te geven, dus het is snel genoeg om als basisgenerator te fungeren.”

De logica lijkt vrij eenvoudig.

Hier is de code die wordt gebruikt om de CLR-functie genaamd GetNums_AdamMachanic2_8192_base te definiëren:

System.Data.SqlTypes gebruiken;System.Collections gebruiken; openbare gedeeltelijke klasse GetNumsAdam2{ private struct row { public long max_base; openbare lange base_add; } [Microsoft.SqlServer.Server.SqlFunction( FillRowMethodName ="GetNums_AdamMachanic2_8192_base_fill", TableDefinition ="max_base int, base_add int")] openbare statische IEnumerable GetNums_AdamMachanic2_8192_64(Sq.ValuInt_64(Sq.ValuInt_64) var max_int =max.Waarde; var min_group =min_int / 8192; var max_group =max_int / 8192; for (; min_group <=max_group; min_group++) { if (min_int> max_int) opbrengstonderbreking; var max_base =8192 - (min_int % 8192); if (min_group ==max_group &&max_int <(((max_int / 8192) + 1) * 8192) - 1) max_base =max_int - min_int + 1; rendementsrendement (nieuwe rij () {max_base =max_base, base_add =min_int}); min_int =(min_groep + 1) * 8192; } } public static void GetNums_AdamMachanic2_8192_base_fill(object o, out long max_base, out long base_add) { var r =(rij)o; max_base =r.max_base; base_add =r.base_add; }};

Ik noemde het VS-project GetNumsAdam2 en plaatste het in het pad C:\Temp\ zoals bij de andere projecten. Dit is de code die ik heb gebruikt om de functie in de testdb-database te implementeren:

-- Create assembly en functionDROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic2_8192_base;DROP ASSEMBLY IF EXISTS GetNumsAdam2;GO CREATE ASSEMBLY GetNumsAdam2 FROM 'C:\Temp\GetNumbin\NumsAdam2\Getlls .GetNums_AdamMachanic2_8192_base(@max_base ALS BIGINT, @add_base ALS BIGINT) RETOURTABEL(max_base BIGINT, base_add BIGINT) ORDER (base_add) ALS EXTERNE NAAM GetNumsAdam2.GetNumsAdam2_Adam_Machanbase> 

 Hier is een voorbeeld voor het gebruik van GetNums_AdamMachanic2_8192_base met het bereik 1 tot 100M:
 
SELECTEER * VAN dbo.GetNums_AdamMachanic2_8192_base(1, 100000000);
 

 Deze code genereert de volgende uitvoer, hier in verkorte vorm weergegeven:
 
max_base base_add-------------------- --------------------8191 18192 81928192 163848192 245768192 32768...8192 999669768192 999751688192 999833608192 99991552257 99999744 (12208 rijen beïnvloed)
 

 Hier is de code met de definitie van de T-SQL-functie GetNums_AdamMachanic2_8192 (afgekort):
 
FUNCTIE MAKEN OF WIJZIGEN dbo.GetNums_AdamMachanic2_8192(@max_base AS BIGINT, @add_base AS BIGINT) RETURNS TABLEASRETURN SELECT TOP (@max_base) V.i + @add_base AS val FROM ( VALUES (0), (1), (2), (3), (4), ... (8187), (8188), (8189), (8190), (8191) ) AS V(i);GO
 

 Belangrijk: Ook hier moet ik benadrukken dat, vergelijkbaar met wat ik zei over de tweede oplossing van Kamil, Adam hier een aanname doet dat het TOP-filter de bovenste rijen zal extraheren op basis van rijweergavevolgorde in de tabelwaarde-constructor, wat niet echt is gegarandeerd. Als u een ORDER BY-component toevoegt om TOP te ondersteunen of het filter wijzigt in een WHERE-filter, krijgt u een deterministisch filter, maar dit kan het prestatieprofiel van de oplossing volledig veranderen. 
 

 Ten slotte is hier de buitenste T-SQL-functie, dbo.GetNums_AdamMachanic2, die de eindgebruiker aanroept om de nummerreeks te krijgen:
 
FUNCTIE MAKEN OF WIJZIGEN dbo.GetNums_AdamMachanic2(@low AS BIGINT =1, @high AS BIGINT) RETURNS TABLEASRETURN SELECTEER Y.val AS n FROM (SELECT max_base, base_add FROM dbo.GetNums_AdamMachanic(2_8192_base) ASlow,high @high X KRUIS TOEPASSEN dbo.GetNums_AdamMachanic2_8192(X.max_base, X.base_add) ALS YGO
 

 Deze functie gebruikt de CROSS APPLY-operator om de binnenste T-SQL-functie dbo.GetNums_AdamMachanic2_8192 toe te passen per rij die wordt geretourneerd door de binnenste CLR-functie dbo.GetNums_AdamMachanic2_8192_base.
 

 Laten we deze oplossing eerst testen met behulp van de aggregaattechniek wanneer de volgorde er niet toe doet:
 
SELECTEER MAX(n) AS mx VANAF dbo.GetNums_AdamMachanic2(1, 100000000);
 

 Ik heb het plan weergegeven in figuur 7 voor deze uitvoering.
 

 Figuur 7:Plan voor de functie dbo.GetNums_AdamMachanic2 
 

 Ik heb de volgende tijdstatistieken voor deze test:
 SQL Server ontleden en compileren :CPU-tijd =313 ms, verstreken tijd =339 ms .
SQL Server uitvoeringstijd :CPU-tijd =8859 ms, verstreken tijd =8849 ms . 

 Logische uitlezingen waren niet nodig.
 

 De uitvoeringstijd is niet slecht, maar let op de hoge compileertijd vanwege de grote tabelwaarde-constructor die wordt gebruikt. Je zou zo'n hoge compileertijd betalen, ongeacht de grootte van het bereik dat je aanvraagt, dus dit is vooral lastig als je de functie gebruikt met zeer kleine bereiken. En deze oplossing is nog steeds langzamer dan de T-SQL-oplossingen. 
 

 Laten we de functie testen met volgorde:
 
VERKLAREN @n ALS GROOT; SELECT @n =n VAN dbo.GetNums_AdamMachanic2(1, 100000000) BESTELLEN DOOR n;
 

 Ik heb het plan weergegeven in figuur 8 voor deze uitvoering.
 

 Figuur 8:Plan voor dbo.GetNums_AdamMachanic2 functie met ORDER BY 
 

 Net als bij de tweede oplossing van Kamil, is een expliciete sortering nodig in het plan, met een aanzienlijke prestatievermindering. Dit zijn de tijdstatistieken die ik voor deze test heb gekregen:
 Uitvoeringstijd:CPU-tijd =54891 ms, verstreken tijd =60981 ms . 

 Bovendien is er nog steeds de hoge compileertijdstraf van ongeveer een derde van een seconde. 
 
Conclusie
 

 Het was interessant om op CLR gebaseerde oplossingen te testen voor de uitdaging van getallenreeksen, omdat veel mensen aanvankelijk aannamen dat de best presterende oplossing waarschijnlijk een op CLR gebaseerde oplossing zal zijn. Kamil en Adam gebruikten vergelijkbare benaderingen, waarbij de eerste poging een eenvoudige lus gebruikt die een teller verhoogt en een rij oplevert met de volgende waarde per iteratie, en de meer geavanceerde tweede poging die CLR- en T-SQL-onderdelen combineert. Persoonlijk voel ik me niet op mijn gemak met het feit dat ze in zowel de tweede oplossing van Kamil als Adam vertrouwden op een niet-deterministisch TOP-filter, en toen ik het in mijn eigen tests naar een deterministisch filter converteerde, had dit een nadelige invloed op de prestaties van de oplossing . Either way, our two T-SQL solutions perform better than the CLR ones, and do not result in explicit sorting in the plan when you need the rows ordered. So I don’t really see the value in pursuing the CLR route any further. Figure 9 has a performance summary of the solutions that I presented in this article.
 

 Figure 9:Time performance comparison 
 

 To me, GetNums_AlanCharlieItzikBatch should be the solution of choice when you require absolutely no I/O footprint, and GetNums_SQKWiki should be preferred when you don’t mind a small I/O footprint. Of course, we can always hope that one day Microsoft will add this critically useful tool as a built-in one, and hopefully if/when they do, it will be a performant solution that supports batch processing and parallelism. So don’t forget to vote for this feature improvement request, and maybe even add your comments for why it’s important for you.
 

 I really enjoyed working on this series. I learned a lot during the process, and hope that you did too.