Wat is de snelste manier om de mediaan te berekenen?

SQL Server is traditioneel teruggekeerd van het bieden van native oplossingen voor enkele van de meest voorkomende statistische vragen, zoals het berekenen van een mediaan. Volgens WikiPedia wordt "mediaan beschreven als de numerieke waarde die de hogere helft van een steekproef, een populatie of een kansverdeling scheidt van de onderste helft. De mediaan van een eindige lijst met getallen kan worden gevonden door alle waarnemingen van laagste waarde naar hoogste waarde en kies de middelste. Als er een even aantal waarnemingen is, is er geen enkele middelste waarde; de ​​mediaan wordt dan meestal gedefinieerd als het gemiddelde van de twee middelste waarden."

In termen van een SQL Server-query, is het belangrijkste dat u daaruit haalt, dat u alle waarden moet "schikken" (sorteren). Sorteren in SQL Server is meestal een vrij dure operatie als er geen ondersteunende index is, en het toevoegen van een index om een ​​operatie te ondersteunen die waarschijnlijk niet wordt gevraagd en die vaak niet de moeite waard is.

Laten we eens kijken hoe we dit probleem doorgaans hebben opgelost in eerdere versies van SQL Server. Laten we eerst een heel eenvoudige tabel maken, zodat we kunnen zien dat onze logica correct is en een nauwkeurige mediaan afleidt. We kunnen de volgende twee tabellen testen, een met een even aantal rijen en de andere met een oneven aantal rijen:

CREATE TABLE dbo.EvenRows ( id INT PRIMARY KEY, val INT );
CREATE TABLE dbo.OddRows  ( id INT PRIMARY KEY, val INT );
 
INSERT dbo.EvenRows(id,val) 
          SELECT 1, 6
UNION ALL SELECT 2, 11
UNION ALL SELECT 3, 4
UNION ALL SELECT 4, 4
UNION ALL SELECT 5, 15
UNION ALL SELECT 6, 14
UNION ALL SELECT 7, 4
UNION ALL SELECT 8, 9;
 
INSERT dbo.OddRows(id,val)
          SELECT 1, 6
UNION ALL SELECT 2, 11
UNION ALL SELECT 3, 4
UNION ALL SELECT 4, 4
UNION ALL SELECT 5, 15
UNION ALL SELECT 6, 14
UNION ALL SELECT 7, 4;
 
DECLARE @Median DECIMAL(12, 2);

Gewoon terloops kunnen we zien dat de mediaan voor de tafel met oneven rijen 6 moet zijn, en voor de even tafel 7,5 ((6+9)/2). Laten we nu eens kijken naar enkele oplossingen die door de jaren heen zijn gebruikt:

SQL Server 2000

In SQL Server 2000 waren we beperkt tot een zeer beperkt T-SQL-dialect. Ik onderzoek deze opties ter vergelijking omdat sommige mensen nog steeds SQL Server 2000 gebruiken en anderen misschien een upgrade hebben uitgevoerd, maar aangezien hun mediaanberekeningen "vroeger" werden geschreven, zou de code er vandaag nog zo kunnen uitzien.

2000_A – max van de ene helft, min van de andere

Deze benadering neemt de hoogste waarde van de eerste 50 procent, de laagste waarde van de laatste 50 procent, en deelt deze vervolgens door twee. Dit werkt voor even of oneven rijen, omdat in het even geval de twee waarden de twee middelste rijen zijn en in het oneven geval de twee waarden eigenlijk uit dezelfde rij komen.

SELECT @Median = (
   (SELECT MAX(val) FROM
     (SELECT TOP 50 PERCENT val 
      FROM dbo.EvenRows ORDER BY val, id) AS t)
 + (SELECT MIN(val) FROM
     (SELECT TOP 50 PERCENT val 
      FROM dbo.EvenRows ORDER BY val DESC, id DESC) AS b)
) / 2.0;

2000_B – #temp tabel

In dit voorbeeld wordt eerst een #temp-tabel gemaakt en met behulp van hetzelfde type wiskunde als hierboven worden de twee "middelste" rijen bepaald met hulp van een aaneengesloten IDENTITY kolom geordend op de kolom val. (De volgorde van toewijzing van IDENTITY waarden kunnen alleen worden vertrouwd vanwege de MAXDOP instelling.)

CREATE TABLE #x
(
  i    INT IDENTITY(1,1),
  val  DECIMAL(12, 2)
);
 
CREATE CLUSTERED INDEX v ON #x(val);
 
INSERT #x(val)
  SELECT val 
  FROM dbo.EvenRows
  ORDER BY val OPTION (MAXDOP 1);
 
SELECT @Median = AVG(val) 
  FROM #x AS x 
  WHERE EXISTS
  (
    SELECT 1 
      FROM #x 
      WHERE x.i - (SELECT  MAX(i) / 2.0 FROM #x) IN (0, 0.5, 1)
  );

SQL Server 2005, 2008, 2008 R2

SQL Server 2005 introduceerde enkele interessante nieuwe vensterfuncties, zoals ROW_NUMBER() , die kan helpen bij het oplossen van statistische problemen zoals mediaan iets gemakkelijker dan we zouden kunnen in SQL Server 2000. Deze benaderingen werken allemaal in SQL Server 2005 en hoger:

2005_A – duellerende rijnummers

Dit voorbeeld gebruikt ROW_NUMBER() om de waarden eenmaal in elke richting op en neer te lopen en vindt vervolgens de "middelste" een of twee rijen op basis van die berekening. Dit lijkt veel op het eerste voorbeeld hierboven, met een eenvoudigere syntaxis:

SELECT @Median = AVG(1.0 * val)
FROM
(
   SELECT val, 
      ra = ROW_NUMBER() OVER (ORDER BY val, id),
      rd = ROW_NUMBER() OVER (ORDER BY val DESC, id DESC)
   FROM dbo.EvenRows
) AS x
WHERE ra BETWEEN rd - 1 AND rd + 1;

2005_B – rijnummer + aantal

Deze lijkt veel op de bovenstaande, met een enkele berekening van ROW_NUMBER() en gebruik dan de totale COUNT() om de "middelste" een of twee rijen te vinden:

SELECT @Median = AVG(1.0 * Val)
FROM 
(
  SELECT val, 
     c  = COUNT(*) OVER (),
     rn = ROW_NUMBER() OVER (ORDER BY val)
  FROM dbo.EvenRows
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2);

2005_C – variatie op rijnummer + aantal

Collega MVP Itzik Ben-Gan liet me deze methode zien, die hetzelfde antwoord oplevert als de bovenstaande twee methoden, maar op een heel iets andere manier:

SELECT @Median = AVG(1.0 * val)
FROM
(
    SELECT o.val, rn = ROW_NUMBER() OVER (ORDER BY o.val), c.c
    FROM dbo.EvenRows AS o
    CROSS JOIN (SELECT c = COUNT(*) FROM dbo.EvenRows) AS c
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2);

SQL Server 2012

In SQL Server 2012 hebben we nieuwe venstermogelijkheden in T-SQL waarmee statistische berekeningen zoals mediaan directer kunnen worden uitgedrukt. Om de mediaan voor een reeks waarden te berekenen, kunnen we PERCENTILE_CONT() gebruiken . We kunnen ook de nieuwe "paging"-extensie gebruiken voor de ORDER BY clausule (OFFSET / FETCH ).

2012_A – nieuwe distributiefunctionaliteit

Deze oplossing maakt gebruik van een zeer eenvoudige berekening met distributie (als u niet het gemiddelde wilt tussen de twee middelste waarden in het geval van een even aantal rijen).

SELECT @Median = PERCENTILE_CONT(0.5) 
  WITHIN GROUP (ORDER BY val) OVER ()
FROM dbo.EvenRows;

2012_B – pagingtruc

Dit voorbeeld implementeert een slim gebruik van OFFSET / FETCH (en niet precies een waarvoor het bedoeld was) - we gaan gewoon naar de rij die één voor de helft van de telling is en nemen dan de volgende één of twee rijen, afhankelijk van of de telling oneven of even was. Met dank aan Itzik Ben-Gan voor het wijzen op deze aanpak.

DECLARE @c BIGINT = (SELECT COUNT(*) FROM dbo.EvenRows);
 
SELECT AVG(1.0 * val)
FROM (
    SELECT val FROM dbo.EvenRows
     ORDER BY val
     OFFSET (@c - 1) / 2 ROWS
     FETCH NEXT 1 + (1 - @c % 2) ROWS ONLY
) AS x;

Maar welke presteert beter?

We hebben geverifieerd dat de bovenstaande methoden allemaal de verwachte resultaten opleveren op onze kleine tafel, en we weten dat de versie van SQL Server 2012 de schoonste en meest logische syntaxis heeft. Maar welke moet u gebruiken in uw drukke productieomgeving? We kunnen een veel grotere tabel bouwen van systeemmetadata, en ervoor zorgen dat we genoeg dubbele waarden hebben. Dit script zal een tabel produceren met 10.000.000 niet-unieke gehele getallen:

USE tempdb;
GO
 
CREATE TABLE dbo.obj(id INT IDENTITY(1,1), val INT);
 
CREATE CLUSTERED INDEX x ON dbo.obj(val, id);
 
INSERT dbo.obj(val) 
SELECT TOP (10000000) o.[object_id]
FROM sys.all_columns AS c 
CROSS JOIN sys.all_objects AS o
CROSS JOIN sys.all_objects AS o2
WHERE o.[object_id] > 0
ORDER BY c.[object_id];

Op mijn systeem zou de mediaan voor deze tabel 146.099.561 moeten zijn. Ik kan dit vrij snel berekenen zonder een handmatige steekproef van 10.000.000 rijen door de volgende query te gebruiken:

SELECT val FROM 
(
    SELECT val, rn = ROW_NUMBER() OVER (ORDER BY val)
    FROM dbo.obj
) AS x 
WHERE rn IN (4999999, 5000000, 5000001);

Resultaten:

val            rn
----           ----
146099561      4999999
146099561      5000000
146099561      5000001

Dus nu kunnen we voor elke methode een opgeslagen procedure maken, controleren of elke methode de juiste uitvoer produceert en vervolgens prestatiestatistieken meten, zoals duur, CPU en uitlezingen. We voeren al deze stappen uit met de bestaande tabel en ook met een kopie van de tabel die niet profiteert van de geclusterde index (we laten deze vallen en maken de tabel opnieuw als een hoop).

Ik heb zeven procedures gemaakt die de bovenstaande querymethoden implementeren. Kortheidshalve zal ik ze hier niet opsommen, maar ze hebben allemaal de naam dbo.Median_<version> , bijv. dbo.Median_2000_A , dbo.Median_2000_B , enz. overeenkomend met de hierboven beschreven benaderingen. Als we deze zeven procedures uitvoeren met behulp van de gratis SQL Sentry Plan Explorer, zien we het volgende in termen van duur, CPU en reads (merk op dat we DBCC FREEPROCCACHE en DBCC DROPCLEANBUFFERS tussen uitvoeringen uitvoeren):

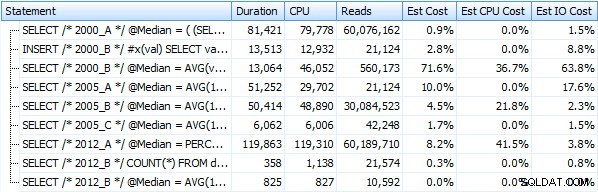
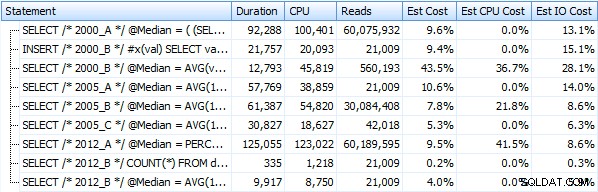
En deze statistieken veranderen helemaal niet veel als we in plaats daarvan tegen een hoop werken. De grootste procentuele verandering was de methode die nog steeds de snelste was:de paging-truc met OFFSET / FETCH:

Hier is een grafische weergave van de resultaten. Om het duidelijker te maken, heb ik de langzaamste uitvoerder in rood gemarkeerd en de snelste nadering in groen.

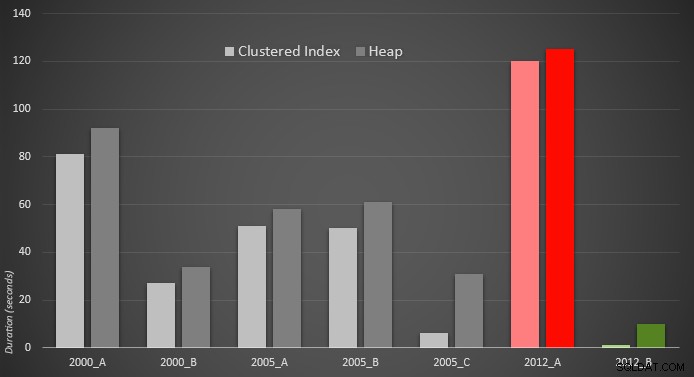
Ik was verrast om te zien dat, in beide gevallen, PERCENTILE_CONT() - die voor dit type berekening is ontworpen - is eigenlijk slechter dan alle andere eerdere oplossingen. Ik denk dat het alleen maar aantoont dat hoewel een nieuwere syntaxis soms onze codering gemakkelijker maakt, dit niet altijd garandeert dat de prestaties zullen verbeteren. Ik was ook verrast om OFFSET / FETCH . te zien blijken zo handig te zijn in scenario's die normaal gesproken niet bij hun doel lijken te passen - paginering.

Ik hoop in ieder geval dat ik heb laten zien welke aanpak je moet gebruiken, afhankelijk van je versie van SQL Server (en dat de keuze hetzelfde moet zijn of je een ondersteunende index voor de berekening hebt).