Dit artikel is het derde in een reeks over optimalisatiedrempels voor het groeperen en aggregeren van gegevens. In deel 1 heb ik het vooraf bestelde Stream Aggregate-algoritme behandeld. In deel 2 heb ik het niet-vooraf bestelde Sort + Stream Aggregate-algoritme behandeld. In dit deel behandel ik het Hash Match (Aggregate) algoritme, dat ik simpelweg Hash Aggregate zal noemen. Ik geef ook een samenvatting en een vergelijking tussen de algoritmen die ik behandel in Deel 1, Deel 2 en Deel 3.
Ik gebruik dezelfde voorbeelddatabase genaamd PerformanceV3, die ik in de vorige artikelen in de serie heb gebruikt. Zorg ervoor dat u, voordat u de voorbeelden in het artikel uitvoert, eerst de volgende code uitvoert om een aantal onnodige indexen te verwijderen:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
De enige twee indexen die in deze tabel moeten worden achtergelaten, zijn idx_cl_od (geclusterd met orderdatum als sleutel) en PK_Orders (niet-geclusterd met orderid als sleutel).
Hash-aggregaat
Het Hash Aggregate-algoritme organiseert de groepen in een hashtabel op basis van een intern gekozen hashfunctie. In tegenstelling tot het Stream Aggregate-algoritme, hoeft het de rijen niet in groepsvolgorde te consumeren. Beschouw de volgende query (we noemen deze Query 1) als voorbeeld (waardoor een hash-aggregatie en een serieel plan wordt geforceerd):
SELECT empid, COUNT(*) AS numorders FROM dbo.Orders GROUP BY empid OPTION (HASH GROUP, MAXDOP 1);
Afbeelding 1 toont het plan voor Query 1.
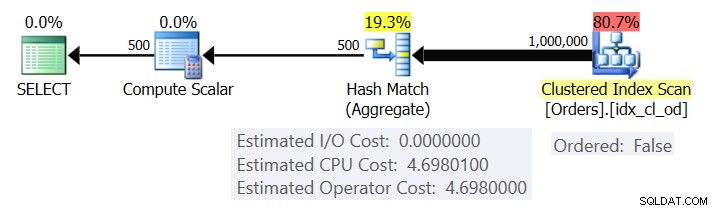
Figuur 1:Plan voor Query 1
Het plan scant de rijen uit de geclusterde index met behulp van een Ordered:False-eigenschap (scan is niet vereist om de rijen te leveren die zijn besteld door de indexsleutel). Doorgaans zal de optimizer de voorkeur geven aan het scannen van de smalste dekkende index, wat in ons geval de geclusterde index is. Het plan bouwt een hashtabel op met de gegroepeerde kolommen en de aggregaten. Onze zoekopdracht vraagt om een INT-getypeerd COUNT-aggregaat. Het plan berekent het eigenlijk als een BIGINT-getypte waarde, vandaar de Compute Scalar-operator, die impliciete conversie toepast op INT.
Microsoft deelt de hash-algoritmen die ze gebruiken niet publiekelijk. Dit is zeer gepatenteerde technologie. Laten we echter, om het concept te illustreren, aannemen dat SQL Server de % 250 (modulo 250) hash-functie gebruikt voor onze bovenstaande query. Voordat we rijen verwerken, heeft onze hashtabel 250 buckets die de 250 mogelijke uitkomsten van de hashfunctie vertegenwoordigen (0 tot en met 249). Terwijl SQL Server elke rij verwerkt, past het de hashfunctie
orderid empid ------- ----- 320 3 30 5 660 253 820 3 850 1 1000 255 700 3 1240 253 350 4 400 255
Afbeelding 2 toont drie toestanden van de hashtabel:voordat er rijen zijn verwerkt, nadat de eerste 5 rijen zijn verwerkt en nadat de eerste 10 rijen zijn verwerkt. Elk item in de gekoppelde lijst bevat de tuple (empid, COUNT(*)).
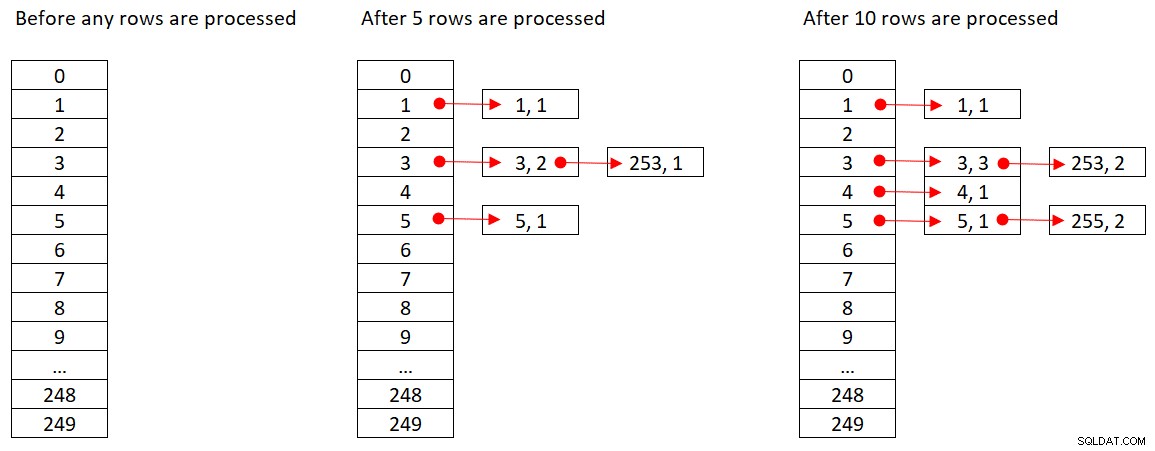
Figuur 2:Hashtabelstatussen
Zodra de Hash Aggregate-operator alle invoerrijen heeft verbruikt, bevat de hashtabel alle groepen met de uiteindelijke status van het aggregaat.
Net als de Sort-operator, vereist de Hash Aggregate-operator een geheugentoekenning, en als het geheugen opraakt, moet het naar tempdb worden gemorst; echter, terwijl sorteren een geheugentoekenning vereist die evenredig is met het aantal rijen dat moet worden gesorteerd, vereist hashing een geheugentoekenning die evenredig is met het aantal groepen. Dus vooral wanneer de groeperingsset een hoge dichtheid heeft (klein aantal groepen), vereist dit algoritme aanzienlijk minder geheugen dan wanneer expliciete sortering vereist is.
Overweeg de volgende twee zoekopdrachten (noem ze Query 1 en Query 2):
SELECT empid, COUNT(*) AS numorders FROM dbo.Orders GROUP BY empid OPTION (HASH GROUP, MAXDOP 1); SELECT empid, COUNT(*) AS numorders FROM dbo.Orders GROUP BY empid OPTION (ORDER GROUP, MAXDOP 1);
Afbeelding 3 vergelijkt de geheugentoekenningen voor deze zoekopdrachten.

Figuur 3:Plannen voor Query 1 en Query 2
Let op het grote verschil tussen de geheugentoekenningen in de twee gevallen.
Wat betreft de kosten van de Hash Aggregate-operator, teruggaand naar figuur 1, merk op dat er geen I/O-kosten zijn, maar alleen CPU-kosten. Probeer vervolgens de CPU-kostenformule te reverse-engineeren met behulp van vergelijkbare technieken als degene die ik in de vorige delen van de serie heb behandeld. De factoren die mogelijk van invloed kunnen zijn op de kosten van de operator, zijn het aantal invoerrijen, het aantal uitvoergroepen, de gebruikte aggregatiefunctie en waarop u groepeert (kardinaliteit van de groeperingsset, gebruikte gegevenstypen).
Je zou verwachten dat deze operator opstartkosten heeft ter voorbereiding op het bouwen van de hashtabel. Je zou ook verwachten dat het lineair zou schalen met betrekking tot het aantal rijen en groepen. Dat is inderdaad wat ik heb gevonden. Hoewel de kosten van zowel de Stream Aggregate- als de Sort-operatoren niet worden beïnvloed door waarop u groepeert, lijkt het erop dat de kosten van de Hash Aggregate-operator dat wel zijn, zowel in termen van de kardinaliteit van de groeperingsset als de gebruikte gegevenstypen.
Om te zien dat de kardinaliteit van de groeperingsset van invloed is op de kosten van de operator, controleert u de CPU-kosten van de Hash Aggregate-operators in de plannen voor de volgende query's (noem ze Query 3 en Query 4):
SELECT orderid % 1000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D GROUP BY orderid % 1000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 50 AS grp1, orderid % 20 AS grp2, MAX(orderdate) AS maxod FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D GROUP BY orderid % 50, orderid % 20 OPTION(HASH GROUP, MAXDOP 1);
Natuurlijk wilt u ervoor zorgen dat het geschatte aantal invoerrijen en uitvoergroepen in beide gevallen hetzelfde is. De geschatte plannen voor deze zoekopdrachten worden weergegeven in figuur 4.

Figuur 4:Plannen voor Query 3 en Query 4
Zoals u kunt zien, bedragen de CPU-kosten van de Hash Aggregate-operator 0,16903 bij groepering op één geheeltallige kolom en 0,174016 bij groepering op twee gehele gehele kolommen, waarbij al het andere gelijk is. Dit betekent dat de kardinaliteit van de groeperingsset inderdaad van invloed is op de kosten.
Wat betreft de vraag of het gegevenstype van het gegroepeerde element de kosten beïnvloedt, heb ik de volgende query's gebruikt om dit te controleren (noem ze Query 5, Query 6 en Query 7):
SELECT CAST(orderid AS SMALLINT) % CAST(1000 AS SMALLINT) AS grp,
MAX(orderdate) AS maxod
FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D
GROUP BY CAST(orderid AS SMALLINT) % CAST(1000 AS SMALLINT)
OPTION(HASH GROUP, MAXDOP 1);
SELECT orderid % 1000 AS grp, MAX(orderdate) AS maxod
FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D
GROUP BY orderid % 1000
OPTION(HASH GROUP, MAXDOP 1);
SELECT CAST(orderid AS BIGINT) % CAST(1000 AS BIGINT) AS grp,
MAX(orderdate) AS maxod
FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D
GROUP BY CAST(orderid AS BIGINT) % CAST(1000 AS BIGINT)
OPTION(HASH GROUP, MAXDOP 1); De plannen voor alle drie de query's hebben hetzelfde geschatte aantal invoerrijen en uitvoergroepen, maar ze krijgen allemaal verschillende geschatte CPU-kosten (0.121766, 0.16903 en 0.171716), vandaar dat het gebruikte gegevenstype wel van invloed is op de kosten.
Het type aggregatiefunctie lijkt ook een impact te hebben op de kosten. Beschouw bijvoorbeeld de volgende twee zoekopdrachten (noem ze Query 8 en Query 9):
SELECT orderid % 1000 AS grp, COUNT(*) AS numorders FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D GROUP BY orderid % 1000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 1000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D GROUP BY orderid % 1000 OPTION(HASH GROUP, MAXDOP 1);
De geschatte CPU-kosten voor de Hash Aggregate in het plan voor Query 8 zijn 0,166344 en in Query 9 0,16903.
Het zou een interessante oefening kunnen zijn om uit te zoeken op welke manier de kardinaliteit van de groeperingsset, de gebruikte gegevenstypen en de gebruikte aggregatiefunctie de kosten precies beïnvloeden; Ik heb dit aspect van de kosten gewoon niet nagestreefd. Dus nadat u een keuze hebt gemaakt voor de groeperingsset en de aggregatiefunctie voor uw query, kunt u de kostprijsberekeningsformule reverse-engineeren. Laten we bijvoorbeeld de CPU-kostenformule voor de Hash Aggregate-operator reverse-engineeren bij het groeperen op een enkele integerkolom en het retourneren van het MAX(orderdate)-aggregaat. De formule zou moeten zijn:
CPU-kosten operator =Met behulp van de technieken die ik in de vorige artikelen van de serie heb gedemonstreerd, kreeg ik de volgende reverse-engineered formule:
CPU-kosten operator =0,017749 + @numrows * 0.00000667857 + @numgroups * 0,0000177087U kunt de nauwkeurigheid van de formule controleren met de volgende vragen:
SELECT orderid % 1000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 1000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 2000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 2000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 3000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D GROUP BY orderid % 3000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 6000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D GROUP BY orderid % 6000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 5000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D GROUP BY orderid % 5000 OPTION(HASH GROUP, MAXDOP 1); SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(HASH GROUP, MAXDOP 1);
Ik krijg de volgende resultaten:
numrows numgroups predictedcost estimatedcost ----------- ----------- -------------- -------------- 100000 1000 0.703315 0.703316 100000 2000 0.721023 0.721024 200000 3000 1.40659 1.40659 200000 6000 1.45972 1.45972 500000 5000 3.44558 3.44558 500000 10000 3.53412 3.53412
De formule lijkt perfect te zijn.
Kostenoverzicht en vergelijking
Nu hebben we de kostprijsformules voor de drie beschikbare strategieën:vooraf bestelde Stream Aggregate, Sort + Stream Aggregate en Hash Aggregate. De volgende tabel vat en vergelijkt de kostenkenmerken van de drie algoritmen:
Gereserveerde stream-aggregaat
Sorteren en streamen samen
Hash-aggregaat
Formule
@numgroups * 0.0000005
Klein aantal rijen:
9.99127891201865E-05 + @numrows * LOG(@numrows) * 2.25061348918698E-06
Groot aantal rijen:
1.35166186417734E-04 + @numrows * LOG(@numrows) * 6.62193536908588E-06
+
@numrows * 0,0000006 +
@numgroups * 0,0000005
@numrows * 0.00000667857 +
@numgroups * 0,0000177087
* Groeperen op enkele integerkolom, retourneert MAX(
Schaal
Opstart-I/O-kosten
Opstartkosten CPU
Volgens deze formules toont figuur 5 de manier waarop elk van de strategieën wordt geschaald voor verschillende aantallen invoerrijen, waarbij een vast aantal groepen van 500 als voorbeeld wordt gebruikt.
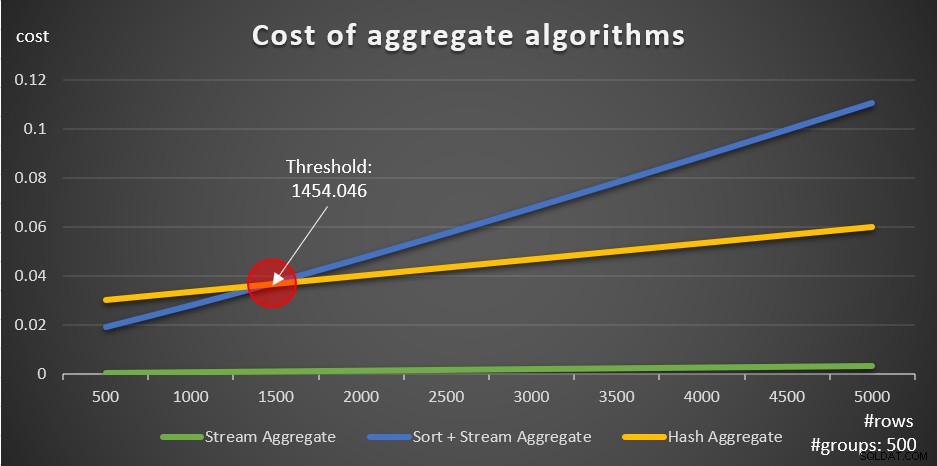
Figuur 5:Kosten van geaggregeerde algoritmen
U kunt duidelijk zien dat als de gegevens vooraf zijn besteld, bijvoorbeeld in een dekkingsindex, de vooraf bestelde Stream Aggregate-strategie de beste optie is, ongeacht het aantal rijen. Stel bijvoorbeeld dat u de tabel Orders moet opvragen en de maximale besteldatum voor elke werknemer moet berekenen. U maakt de volgende dekkingsindex aan:
CREATE INDEX idx_eid_od ON dbo.Orders(empid, orderdate);
Hier zijn vijf zoekopdrachten die een tabel Orders emuleren met verschillende aantallen rijen (10.000, 20.000, 30.000, 40.000 en 50.000):
SELECT empid, MAX(orderdate) AS maxod FROM (SELECT TOP (10000) * FROM dbo.Orders) AS D GROUP BY empid; SELECT empid, MAX(orderdate) AS maxod FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D GROUP BY empid; SELECT empid, MAX(orderdate) AS maxod FROM (SELECT TOP (30000) * FROM dbo.Orders) AS D GROUP BY empid; SELECT empid, MAX(orderdate) AS maxod FROM (SELECT TOP (40000) * FROM dbo.Orders) AS D GROUP BY empid; SELECT empid, MAX(orderdate) AS maxod FROM (SELECT TOP (50000) * FROM dbo.Orders) AS D GROUP BY empid;
Afbeelding 6 toont de plannen voor deze zoekopdrachten.
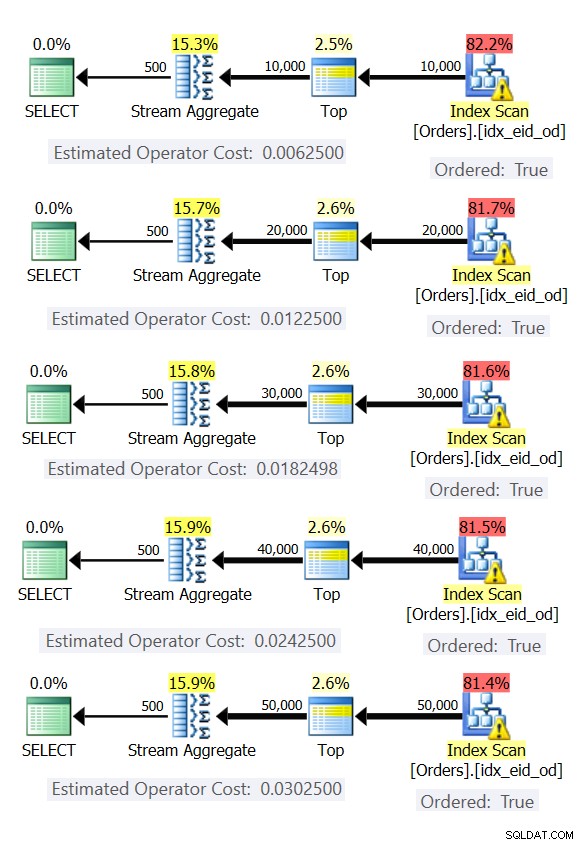
Figuur 6:Plannen met vooraf bestelde Stream Aggregate-strategie
In alle gevallen voeren de plannen een geordende scan uit van de dekkingsindex en passen ze de Stream Aggregate-operator toe zonder dat expliciete sortering nodig is.
Gebruik de volgende code om de index te verwijderen die u voor dit voorbeeld hebt gemaakt:
DROP INDEX idx_eid_od ON dbo.Orders;
Het andere belangrijke om op te merken over de grafieken in figuur 5 is wat er gebeurt als de gegevens niet vooraf zijn besteld. Dit gebeurt wanneer er geen dekkingsindex aanwezig is, en ook wanneer u groepeert op gemanipuleerde uitdrukkingen in plaats van op basiskolommen. Er is een optimalisatiedrempel - in ons geval 1454.046 rijen - waaronder de Sort + Stream Aggregate-strategie lagere kosten heeft en waarop of waarboven de Hash Aggregate-strategie lagere kosten heeft. Dit heeft te maken met het feit dat de eerste hash lagere opstartkosten, maar schaalt op een n log n manier, terwijl de laatste hogere opstartkosten heeft maar lineair schaalt. Dit maakt de eerste de voorkeur met een klein aantal invoerrijen. Als onze reverse-engineering formules juist zijn, zouden de volgende twee zoekopdrachten (noem ze Query 10 en Query 11) verschillende plannen moeten krijgen:
SELECT orderid % 500 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (1454) * FROM dbo.Orders) AS D GROUP BY orderid % 500; SELECT orderid % 500 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (1455) * FROM dbo.Orders) AS D GROUP BY orderid % 500;
De plannen voor deze zoekopdrachten worden weergegeven in figuur 7.
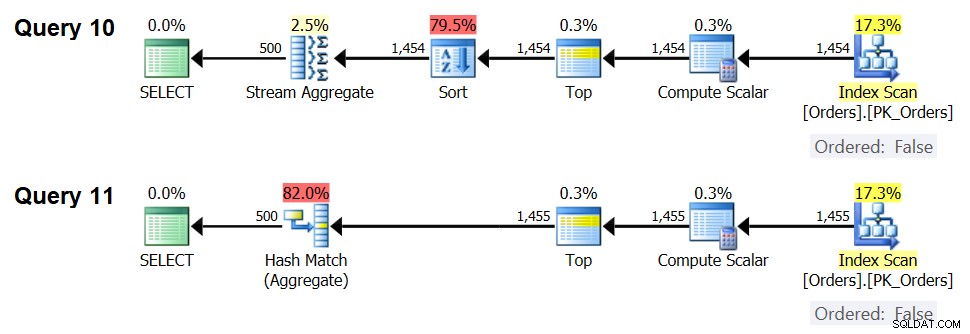
Figuur 7:Plannen voor Query 10 en Query 11
Inderdaad, met 1.454 invoerrijen (onder de optimalisatiedrempel) geeft de optimizer natuurlijk de voorkeur aan het Sort + Stream Aggregate-algoritme voor Query 10, en met 1.455 invoerrijen (boven de optimalisatiedrempel) geeft de optimizer natuurlijk de voorkeur aan het Hash Aggregate-algoritme voor Query 11 .
Potentieel voor Adaptive Aggregate-operator
Een van de lastige aspecten van optimalisatiedrempels zijn problemen met het snuiven van parameters bij het gebruik van parametergevoelige query's in opgeslagen procedures. Beschouw de volgende opgeslagen procedure als voorbeeld:
CREATE OR ALTER PROC dbo.EmpOrders @initialorderid AS INT AS SELECT empid, COUNT(*) AS numorders FROM dbo.Orders WHERE orderid >= @initialorderid GROUP BY empid; GO
U maakt de volgende optimale index om de opgeslagen procedurequery te ondersteunen:
CREATE INDEX idx_oid_i_eid ON dbo.Orders(orderid) INCLUDE(empid);
U hebt de index gemaakt met orderid als sleutel om het bereikfilter van de query te ondersteunen, en empid voor dekking opgenomen. Dit is een situatie waarin u niet echt een index kunt maken die zowel het bereikfilter ondersteunt als de gefilterde rijen voorgeordend door de groeperingsset. Dit betekent dat de optimizer een keuze zal moeten maken tussen de Sort + stream Aggregate en de Hash Aggregate algoritmen. Op basis van onze kostenformules ligt de optimalisatiedrempel tussen 937 en 938 invoerrijen (laten we zeggen 937,5 rijen).
Stel dat u de opgeslagen procedure de eerste keer uitvoert met een ingevoerde initiële order-ID die u een klein aantal overeenkomsten geeft (onder de drempel):
EXEC dbo.EmpOrders @initialorderid = 999991;
SQL Server produceert een plan dat gebruikmaakt van het Sort + Stream Aggregate-algoritme en slaat het plan op in de cache. Bij volgende uitvoeringen wordt het in de cache opgeslagen plan opnieuw gebruikt, ongeacht het aantal rijen dat erbij betrokken is. De volgende uitvoering heeft bijvoorbeeld een aantal overeenkomsten boven de optimalisatiedrempel:
EXEC dbo.EmpOrders @initialorderid = 990001;
Toch hergebruikt het het in de cache opgeslagen plan, ondanks het feit dat het niet optimaal is voor deze uitvoering. Dat is een klassiek probleem met het snuiven van parameters.
SQL Server 2017 introduceert adaptieve queryverwerkingsmogelijkheden, die zijn ontworpen om met dergelijke situaties om te gaan door tijdens het uitvoeren van de query te bepalen welke strategie moet worden gebruikt. Een van die verbeteringen is een Adaptive Join-operator die tijdens de uitvoering bepaalt of een Loop- of Hash-algoritme moet worden geactiveerd op basis van een berekende optimalisatiedrempel. Ons geaggregeerde verhaal smeekt om een vergelijkbare Adaptive Aggregate-operator, die tijdens de uitvoering een keuze zou maken tussen een Sort + Stream Aggregate-strategie en een Hash Aggregate-strategie, op basis van een berekende optimalisatiedrempel. Afbeelding 8 illustreert een pseudoplan op basis van dit idee.
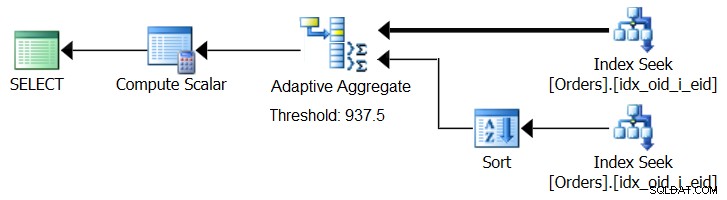
Figuur 8:Pseudo-abonnement met Adaptive Aggregate-operator
Voor nu, om zo'n plan te krijgen, moet je Microsoft Paint gebruiken. Maar aangezien het concept van adaptieve queryverwerking zo slim is en zo goed werkt, is het niet meer dan redelijk om in de toekomst verdere verbeteringen op dit gebied te verwachten.
Voer de volgende code uit om de index te verwijderen die u voor dit voorbeeld hebt gemaakt:
DROP INDEX idx_oid_i_eid ON dbo.Orders;
Conclusie
In dit artikel heb ik de kostenberekening en schaling van het Hash Aggregate-algoritme behandeld en deze vergeleken met de strategieën Stream Aggregate en Sort + Stream Aggregate. Ik heb de optimalisatiedrempel beschreven die bestaat tussen de Sort + Stream Aggregate- en Hash Aggregate-strategieën. Bij kleine aantallen invoerrijen heeft de eerste de voorkeur en bij grote aantallen de laatste. Ik beschreef ook het potentieel voor het toevoegen van een Adaptive Aggregate-operator, vergelijkbaar met de reeds geïmplementeerde Adaptive Join-operator, om problemen met parameter-sniffing op te lossen bij het gebruik van parametergevoelige queries. Volgende maand zal ik de discussie voortzetten door parallellisme-overwegingen en gevallen te behandelen die vragen om herschrijvingen.
