Vorige maand heb ik Peter Larsson's puzzel van het matchen van vraag en aanbod behandeld. Ik liet Peters rechttoe rechtaan op cursor gebaseerde oplossing zien en legde uit dat deze lineair geschaald is. De uitdaging waarmee ik je achterliet, is om te proberen met een set-gebaseerde oplossing voor de taak te komen, en jongen, laat mensen de uitdaging aangaan! Bedankt Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie en natuurlijk Peter Larsson voor het sturen van jullie oplossingen. Sommige ideeën waren briljant en ronduit verbluffend.
Deze maand ga ik beginnen met het verkennen van de ingediende oplossingen, ruwweg, van de slechtst presterende naar de best presterende. Waarom zou je je zelfs druk maken over de slecht presterende? Want je kunt er nog veel van leren; bijvoorbeeld door anti-patronen te identificeren. Inderdaad, de eerste poging om deze uitdaging voor veel mensen op te lossen, waaronder ikzelf en Peter, is gebaseerd op een interval-intersectieconcept. Het is zo dat de klassieke, op predikaten gebaseerde techniek voor het identificeren van intervallen van intervallen slecht presteert omdat er geen goed indexeringsschema is om dit te ondersteunen. Dit artikel is gewijd aan deze slecht presterende aanpak. Ondanks de matige performance is het werken aan de oplossing een interessante oefening. Het vereist het oefenen van de vaardigheid om het probleem te modelleren op een manier die zich leent voor een set-gebaseerde behandeling. Het is ook interessant om de reden voor de slechte prestaties te identificeren, waardoor het anti-patroon in de toekomst gemakkelijker kan worden vermeden. Houd er rekening mee dat deze oplossing slechts het startpunt is.
DDL en een kleine set voorbeeldgegevens
Ter herinnering:de taak omvat het opvragen van een tabel met de naam 'Veilingen'. Gebruik de volgende code om de tabel te maken en deze te vullen met een kleine set voorbeeldgegevens:
DROP TABEL INDIEN BESTAAT dbo.Auctions; MAAK TABEL dbo.Auctions( ID INT NOT NULL IDENTITY(1, 1) CONSTRAINT pk_Auctions PRIMARY KEY CLUSTERED, Code CHAR(1) NOT NULL CONSTRAINT ck_Auctions_Code CHECK (Code ='D' OR Code ='S'), Hoeveelheid DECIMAL(19 , 6) NIET NULL CONSTRAINT ck_Auctions_Quantity CHECK (Aantal> 0)); STEL GEEN AANTAL IN; VERWIJDEREN VAN dbo.Veilingen; SET IDENTITY_INSERT dbo.Veilingen AAN; INSERT INTO dbo.Auctions (ID, Code, Hoeveelheid) WAARDEN (1, 'D', 5.0), (2, 'D', 3.0), (3, 'D', 8.0), (5, 'D', 2.0), (6, 'D', 8.0), (7, 'D', 4.0), (8, 'D', 2.0), (1000, 'S', 8.0), (2000, 'S', 6.0), (3000, 'S', 2.0), (4000, 'S', 2.0), (5000, 'S', 4.0), (6000, 'S', 3.0), (7000, 'S', 2.0); SET IDENTITY_INSERT dbo.Veilingen UIT;
Het was jouw taak om koppelingen te maken die het aanbod matchen met de vraag op basis van ID-bestelling, en deze naar een tijdelijke tabel te schrijven. Hieronder volgt het gewenste resultaat voor de kleine set voorbeeldgegevens:
DemandID SupplyID TradeQuantity----------- ----------- --------------1 1000 5.0000002 1000 3.0000003 2000 6.0000003 3000 2.0000005 4000 2.0000006 5000 4.0000006 6000 3.0000006 7000 1.0000007 7000 1.000000
Vorige maand heb ik ook code geleverd die u kunt gebruiken om de veilingentabel te vullen met een grote set voorbeeldgegevens, waarbij u het aantal invoer- en vraaginvoeren en hun reeks hoeveelheden controleert. Zorg ervoor dat u de code uit het artikel van vorige maand gebruikt om de prestaties van de oplossingen te controleren.
De gegevens modelleren als intervallen
Een intrigerend idee dat zich leent voor het ondersteunen van op sets gebaseerde oplossingen, is om de gegevens als intervallen te modelleren. Met andere woorden, geef elke invoer voor vraag en aanbod weer als een interval, beginnend met de lopende totale hoeveelheden van dezelfde soort (vraag of aanbod) tot maar exclusief de huidige, en eindigend met het lopende totaal inclusief de huidige, natuurlijk op basis van ID bestellen. Als u bijvoorbeeld naar de kleine set voorbeeldgegevens kijkt, is de eerste vraaginvoer (ID 1) voor een hoeveelheid van 5,0 en de tweede (ID 2) voor een hoeveelheid van 3,0. De eerste vraaginvoer kan worden weergegeven met de intervalstart:0,0, eind:5,0 en de tweede met de intervalstart:5,0, eind:8,0, enzovoort.
Evenzo, de eerste leveringsinvoer (ID 1000) is voor een hoeveelheid van 8,0 en de tweede (ID 2000) is voor een hoeveelheid van 6,0. De eerste invoer kan worden weergegeven met het interval start:0,0, einde:8,0 en de tweede met het interval start:8,0, einde:14,0, enzovoort.
De vraag-aanbod-koppelingen die u moet maken, zijn dan de overlappende segmenten van de kruisende intervallen tussen de twee soorten.
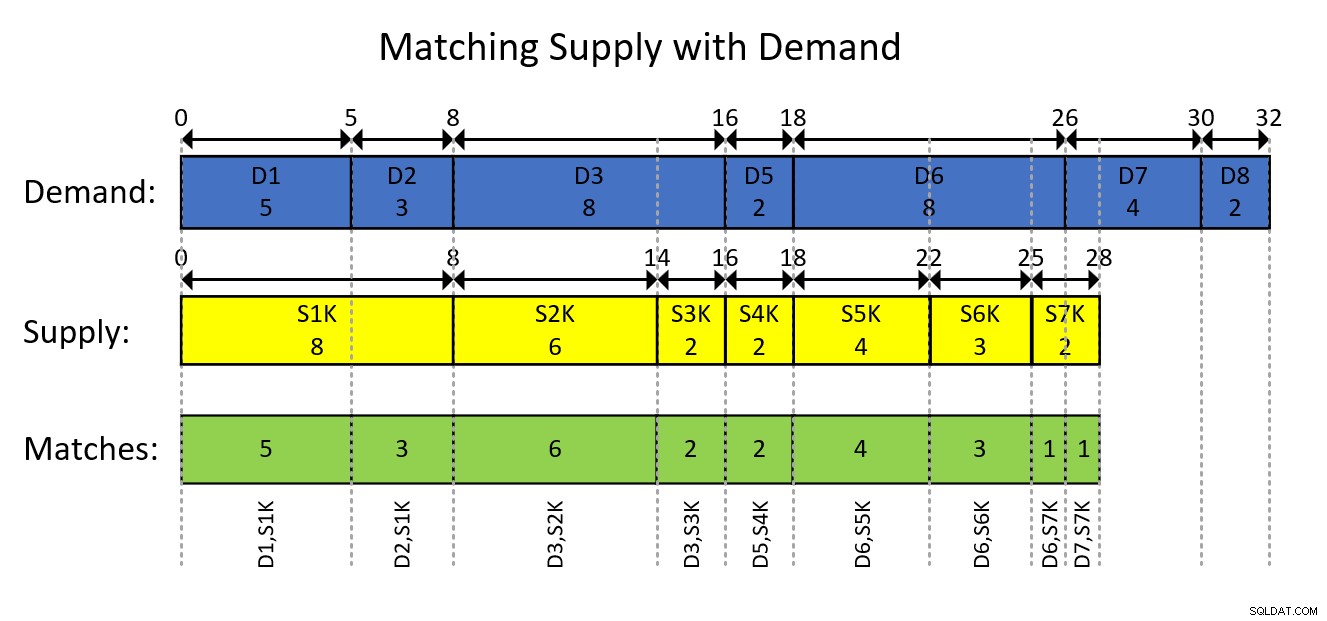
Dit wordt waarschijnlijk het best begrepen met een visuele weergave van de op interval gebaseerde modellering van de gegevens en het gewenste resultaat, zoals weergegeven in figuur 1.
 Figuur 1:Modelleren van de gegevens als intervallen
Figuur 1:Modelleren van de gegevens als intervallen
De visuele weergave in figuur 1 spreekt voor zich, maar kortom...
De blauwe rechthoeken vertegenwoordigen de vraaginvoer als intervallen, waarbij de exclusieve lopende totale hoeveelheden worden weergegeven als het begin van het interval en het inclusief lopende totaal als het einde van het interval. De gele rechthoeken doen hetzelfde voor aanbodinvoer. Merk vervolgens op hoe de overlappende segmenten van de elkaar kruisende intervallen van de twee soorten, die worden weergegeven door de groene rechthoeken, de vraag-aanbod-combinaties zijn die u moet produceren. De eerste resultaatkoppeling is bijvoorbeeld met vraag-ID 1, aanbod-ID 1000, hoeveelheid 5. De tweede resultaatkoppeling is met vraag-ID 2, aanbod-ID 1000, hoeveelheid 3. enzovoort.
Interval-intersecties met behulp van CTE's
Voordat u begint met het schrijven van de T-SQL-code met oplossingen op basis van het idee van intervalmodellering, moet u al een intuïtief gevoel hebben voor welke indexen hier waarschijnlijk nuttig zijn. Aangezien u waarschijnlijk vensterfuncties gebruikt om lopende totalen te berekenen, kunt u profiteren van een dekkende index met een sleutel op basis van de kolommen Code, ID en inclusief de kolom Hoeveelheid. Hier is de code om zo'n index te maken:
MAAK UNIEKE NIET-GECLUSTERDE INDEX idx_Code_ID_i_Quantity OP dbo.Auctions(Code, ID) INCLUDE(Quantity);
Dat is dezelfde index die ik heb aanbevolen voor de cursorgebaseerde oplossing die ik vorige maand heb behandeld.
Ook is er hier potentieel om te profiteren van batchverwerking. U kunt de overweging inschakelen zonder de vereisten van batchmodus in rowstore, bijvoorbeeld met SQL Server 2019 Enterprise of hoger, door de volgende dummy columnstore-index te maken:
MAAK NIET-GECLUSTERDE KOLOMSTORE INDEX idx_cs OP dbo.Auctions(ID) WHERE ID =-1 AND ID =-2;
U kunt nu aan de T-SQL-code van de oplossing gaan werken.
De volgende code creëert de intervallen die de vraaginvoer vertegenwoordigen:
MET D0 AS-- D0 berekent de lopende vraag als EndDemand(SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D haalt prev EndDemand uit als StartDemand, waarbij de start-end-vraag wordt uitgedrukt als een intervalD AS( SELECT ID, Hoeveelheid, EndDemand - Hoeveelheid AS StartDemand, EndDemand FROM D0)SELECT *FROM D;
De query die de CTE D0 definieert, filtert vraagitems uit de tabel Veilingen en berekent een lopende totale hoeveelheid als het eindscheidingsteken van de vraagintervallen. Vervolgens noemt de query die de tweede CTE definieert, D-query's D0 en berekent het beginscheidingsteken van de vraagintervallen door de huidige hoeveelheid af te trekken van het eindscheidingsteken.
Deze code genereert de volgende uitvoer:
ID Hoeveelheid StartDemand EndDemand---- --------- ------------ ----------1 5.000000 0.000000 5.0000002 3.000000 5.000000 8.0000003 8.000000 8.000000 16.0000005 2.000000 16.000000 18.0000006 8.000000 18.000000 26.0000007 4.000000 26.000000 30.0000008 2.000000 30.000000 32.000000
De leveringsintervallen worden op dezelfde manier gegenereerd door dezelfde logica toe te passen op de leveringsitems, met behulp van de volgende code:
MET S0 AS-- S0 berekent het lopende aanbod als EndSupply(SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extracten prev EndSupply als StartSupply, waarbij de start-end-levering wordt uitgedrukt als een intervalS AS(SELECT ID, Quantity, EndSupply - Aantal AS StartSupply, EndSupply FROM S0)SELECT *FROM S;
Deze code genereert de volgende uitvoer:
ID Aantal StartSupply EndSupply----- --------- ------------ ----------1000 8.000000 0.000000 8.0000002000 6.000000 8.000000 14.0000003000 2.000000 14.000000 16.0000004000 2.000000 16.000000 18.0000005000 4.000000 18.000000 22.0000006000 3.000000 22.000000 25.0000007000 2.000000 25.000000 27.000000
Wat overblijft is dan om de kruisende vraag- en aanbodintervallen van de CTE's D en S te identificeren en de overlappende segmenten van die kruisende intervallen te berekenen. Onthoud dat de resultaatparen in een tijdelijke tabel moeten worden geschreven. Dit kan met de volgende code:
-- Laat de temp-tabel vallen als deze bestaat DROP TABLE IF EXISTS #MyPairings; WITH D0 AS-- D0 berekent de lopende vraag als EndDemand(SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extracten prev EndDemand als StartDemand, waarbij de begin-eindvraag wordt uitgedrukt als een intervalD AS(SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0),S0 AS-- S0 berekent het lopende aanbod als EndSupply(SELECT ID, Quantity, SUM(Quantity) OVER (ORDER BY ID RIJEN ONGEBONDEN VOORAFGAANDE) AS EndSupply VAN dbo.Auctions WHERE Code ='S'),-- S extracten prev EndSupply als StartSupply, waarbij de start-end supply wordt uitgedrukt als een intervalS AS( SELECT ID, Hoeveelheid, EndSupply - Hoeveelheid AS StartSupply, EndSupply FROM S0)-- De buitenste query identificeert transacties als de overlappende segmenten van de elkaar kruisende intervallen. D.ID AS DemandID, S.ID AS SupplyID, CASE WH EN EndDemandStartSupply DAN StartDemand ELSE StartSupply EINDE AS TradeQuantityINTO #MyPairingsFROM D INNER JOIN S ON D.StartDemand S.StartDemand; Naast de code die de vraag- en aanbodintervallen maakt, die je al eerder zag, is de belangrijkste toevoeging hier de buitenste query, die de kruisende intervallen tussen D en S identificeert en de overlappende segmenten berekent. Om de kruisende intervallen te identificeren, voegt de buitenste query D en S samen met behulp van het volgende join-predikaat:
D.StartDemandS.StartSupply Dat is het klassieke predikaat om intervallen te identificeren. Het is ook de belangrijkste oorzaak van de slechte prestaties van de oplossing, zoals ik binnenkort zal uitleggen.
De buitenste query berekent ook de handelshoeveelheid in de SELECT-lijst als:
LEAST(EndDemand, EndSupply) - GREATEST(StartDemand, StartSupply)Als u Azure SQL gebruikt, kunt u deze expressie gebruiken. Als u SQL Server 2019 of eerder gebruikt, kunt u het volgende logisch equivalente alternatief gebruiken:
CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply EINDE Aangezien de vereiste was om het resultaat in een tijdelijke tabel te schrijven, gebruikt de buitenste query een SELECT INTO-instructie om dit te bereiken.
Het idee om de gegevens te modelleren als intervallen is duidelijk intrigerend en elegant. Maar hoe zit het met de prestaties? Helaas heeft deze specifieke oplossing een groot probleem met betrekking tot de identificatie van intervallen. Bekijk het plan voor deze oplossing in figuur 2.
Figuur 2:Queryplan voor kruispunten met CTE-oplossing
Laten we beginnen met de goedkope onderdelen van het plan.
De buitenste invoer van de Nested Loops-join berekent de vraagintervallen. Het gebruikt een Index Seek-operator om de vraaginvoer op te halen, en een batch-modus Window Aggregate-operator om het scheidingsteken voor het einde van het vraaginterval te berekenen (in dit plan Expr1005 genoemd). Het beginscheidingsteken voor het vraaginterval is dan Uitdr1005 – Hoeveelheid (vanaf D).
Een kanttekening is dat je het gebruik van een expliciete Sort-operator voorafgaand aan de batch-modus Window Aggregate-operator hier verrassend vindt, omdat de vraagitems die uit de Index Seek worden opgehaald, al op ID zijn gerangschikt, zoals de vensterfunctie ze nodig heeft. Dit heeft te maken met het feit dat SQL Server momenteel geen efficiënte combinatie van parallelle indexbewerkingen voor het behouden van orders ondersteunt voorafgaand aan een parallelle batch-modus Window Aggregate-operator. Als u een serieel plan alleen voor experimentele doeleinden forceert, ziet u de sorteeroperator verdwijnen. SQL Server besloot over het algemeen dat het gebruik van parallellisme hier de voorkeur had, ondanks dat dit resulteerde in de toegevoegde expliciete sortering. Maar nogmaals, dit deel van het plan vertegenwoordigt een klein deel van het werk in het grote geheel.
Evenzo begint de binnenste invoer van de Nested Loops-verbinding met het berekenen van de toevoerintervallen. Vreemd genoeg koos SQL Server ervoor om rijmodusoperators te gebruiken om dit onderdeel af te handelen. Aan de ene kant brengen rijmodusoperators die worden gebruikt om lopende totalen te berekenen, meer overhead met zich mee dan het batchmodus Window Aggregate-alternatief; aan de andere kant heeft SQL Server een efficiënte parallelle implementatie van een indexbewerking die de volgorde behoudt, gevolgd door de berekening van de vensterfunctie, waardoor expliciete sortering voor dit onderdeel wordt vermeden. Het is merkwaardig dat de optimizer een strategie heeft gekozen voor de vraagintervallen en een andere voor de aanbodintervallen. In ieder geval haalt de Index Seek-operator de leveringsitems op en de daaropvolgende reeks operators tot aan de Compute Scalar-operator berekent het einde van het leveringsinterval (in dit plan aangeduid als Expr1009). Het startbegrenzingsteken voor het leveringsinterval is dan Uitdr1009 – Hoeveelheid (vanaf S).
Ondanks de hoeveelheid tekst die ik heb gebruikt om deze twee delen te beschrijven, is het echt dure deel van het werk in het plan wat daarna komt.
Het volgende deel moet de vraagintervallen en de aanbodintervallen samenvoegen met behulp van het volgende predikaat:
D.StartDemandS.StartSupply Zonder ondersteunende index, uitgaande van DI-vraagintervallen en SI-toevoerintervallen, zou dit de verwerking van DI * SI-rijen met zich meebrengen. Het plan in figuur 2 is gemaakt na het vullen van de veilingtabel met 400.000 rijen (200.000 vraaginvoeren en 200.000 leveringsinvoeren). Dus zonder ondersteunende index zou het plan 200.000 * 200.000 =40.000.000.000 rijen hebben moeten verwerken. Om deze kosten te beperken, koos de optimizer ervoor om een tijdelijke index te maken (zie de Index Spool-operator) met het eindscheidingsteken voor het leveringsinterval (Expr1009) als sleutel. Dat is zo'n beetje het beste wat het kon doen. Dit lost echter slechts een deel van het probleem op. Met twee bereikpredikaten kan er slechts één worden ondersteund door een indexzoekpredikaat. De andere moet worden afgehandeld met behulp van een residuaal predikaat. U kunt inderdaad in het plan zien dat de seek in de tijdelijke index het seek-predikaat Expr1009> Expr1005 – D.Quantity gebruikt, gevolgd door een Filter-operator die het resterende predikaat Expr1005> Expr1009 – S.Quantity hanteert.
Ervan uitgaande dat het zoekpredikaat gemiddeld de helft van de aanbodrijen isoleert van de index per vraagrij, is het totale aantal rijen dat wordt uitgezonden door de Index Spool-operator en verwerkt door de Filter-operator dan DI * SI / 2. In ons geval, met 200.000 vraagrijen en 200.000 aanbodrijen, dit vertaalt zich naar 20.000.000.000. Inderdaad, de rij die van de operator Index Spool naar de operator Filter gaat, meldt een aantal rijen die hier dicht bij liggen.
Dit plan heeft kwadratische schaling, vergeleken met de lineaire schaling van de cursorgebaseerde oplossing van vorige maand. Je kunt het resultaat zien van een prestatietest waarin de twee oplossingen worden vergeleken in figuur 3. Je kunt duidelijk de mooi gevormde parabool zien voor de set-gebaseerde oplossing.
Figuur 3:Prestaties van kruispunten met CTE-oplossing versus cursorgebaseerde oplossing
Interval-intersecties met behulp van tijdelijke tabellen
U kunt de zaken enigszins verbeteren door het gebruik van CTE's voor de vraag- en aanbodintervallen te vervangen door tijdelijke tabellen, en om de indexspoel te vermijden, door uw eigen index op de tijdelijke tabel te maken met de leveringsintervallen met het eindscheidingsteken als de sleutel. Hier is de code van de volledige oplossing:
-- Laat tijdelijke tabellen vallen indien aanwezigDROP TABLE IF BESTAAT #MyPairings, #Demand, #Supply; WITH D0 AS-- D0 berekent de lopende vraag als EndDemand(SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extracten prev EndDemand as StartDemand, die de begin-eindvraag uitdrukt als een intervalD AS( SELECT ID, Quantity, EndDemand - Hoeveelheid AS StartDemand, EndDemand FROM D0)SELECT ID, Quantity, CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand, CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemandINTO #DemandFROM D;WITH S0 AS-- S0 berekent het lopende aanbod als EndSupply(SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID RIJEN ONGEBONDEN VOORAFGAAND aan) AS EndSupply VAN dbo.Auctions WHERE Code ='S'),-- S extraheert prev EndSupply als StartSupply, waarbij begin-eindaanvoer wordt uitgedrukt als een interval AS( SELECT ID, Hoeveelheid, EndSupply - Hoeveelheid AS StartSupply, EndSupply FROM S0)SELECT ID, Hoeveelheid, CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply, CAST(ISNULL(EndSupply, 0.0) ALS DECIMAAL (19, 6)) ALS EndSupplyINTO #SupplyFROM S; MAAK UNIEKE GECLUSTERDE INDEX idx_cl_ES_ID OP #Supply(EndSupply, ID); -- Outer query identificeert transacties als de overlappende segmenten van de kruisende intervallen -- In de kruisende vraag- en aanbodintervallen is de handelshoeveelheid dan -- LEAST (EndDemand, EndSupply) - GREATEST (StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM #Demand AS D INNER JOIN #Supply A S S MET S.EndSupply EN D.EndDemand> S.StartSupply; De plannen voor deze oplossing zijn weergegeven in figuur 4:
Figuur 4:Queryplan voor kruispunten met tijdelijke tabellen Oplossing
De eerste twee plannen gebruiken een combinatie van batch-modus Index Seek + Sort + Window Aggregate-operators om de vraag- en aanbodintervallen te berekenen en deze naar tijdelijke tabellen te schrijven. Het derde plan handelt de indexcreatie af op de #Supply-tabel met het EndSupply-scheidingsteken als leidende sleutel.
Het vierde plan vertegenwoordigt verreweg het grootste deel van het werk, met een Nested Loops join-operator die overeenkomt met elk interval van #Demand, de elkaar kruisende intervallen van #Supply. Merk op dat ook hier de Index Seek-operator vertrouwt op het predikaat #Supply.EndSupply> #Demand.StartDemand als het zoekpredikaat en #Demand.EndDemand> #Supply.StartSupply als het resterende predikaat. Dus qua complexiteit/schaalbaarheid krijg je dezelfde kwadratische complexiteit als bij de vorige oplossing. U betaalt gewoon minder per rij omdat u uw eigen index gebruikt in plaats van de indexspoel die door het vorige abonnement werd gebruikt. U kunt de prestaties van deze oplossing zien in vergelijking met de vorige twee in afbeelding 5.
Figuur 5:Prestaties van kruispunten met tijdelijke tabellen in vergelijking met andere twee oplossingen
Zoals je kunt zien, presteert de oplossing met de tijdelijke tabellen beter dan die met de CTE's, maar het heeft nog steeds kwadratische schaling en doet het erg slecht in vergelijking met de cursor.
Wat nu?
Dit artikel behandelt de eerste poging om de klassieke taak om vraag en aanbod te matchen af te handelen met behulp van een setgebaseerde oplossing. Het idee was om de gegevens te modelleren als intervallen, het aanbod af te stemmen op de vraag door kruisende vraag- en aanbodintervallen te identificeren, en vervolgens de handelshoeveelheid te berekenen op basis van de grootte van de overlappende segmenten. Zeker een intrigerend idee. Het grootste probleem ermee is ook het klassieke probleem van het identificeren van intervallen door twee bereikpredikaten te gebruiken. Zelfs als de beste index aanwezig is, kunt u slechts één bereikpredikaat ondersteunen met een indexzoekopdracht; het andere bereikpredikaat moet worden behandeld met een residuaal predikaat. Dit resulteert in een plan met kwadratische complexiteit.
Dus wat kun je doen om dit obstakel te overwinnen? Er zijn verschillende ideeën. Een briljant idee is van Joe Obbish, waarover je uitgebreid kunt lezen in zijn blogpost. Ik zal andere ideeën behandelen in komende artikelen in de serie.
[ Ga naar:Originele uitdaging | Oplossingen:Deel 1 | Deel 2 | Deel 3 ]
