Wanneer SQL Server een query optimaliseert, produceert het tijdens een verkenningsfase kandidaatplannen en kiest daaruit degene met de laagste kosten. Het gekozen plan wordt verondersteld de laagste looptijd te hebben van de onderzochte plannen. Het punt is dat de optimizer alleen kan kiezen tussen strategieën die erin zijn gecodeerd. Bij het optimaliseren van groepering en aggregatie kan de optimizer op de datum van dit schrijven bijvoorbeeld alleen kiezen tussen Stream Aggregate- en Hash Aggregate-strategieën. Ik heb de beschikbare strategieën in eerdere delen van deze serie besproken. In deel 1 heb ik de vooraf bestelde Stream Aggregate-strategie behandeld, in Deel 2 de Sort + Stream Aggregate-strategie, in Deel 3 de Hash Aggregate-strategie en in Deel 4 parallellisme-overwegingen.
Wat de SQL Server-optimizer momenteel niet ondersteunt, is maatwerk en kunstmatige intelligentie. Dat wil zeggen, als je een strategie kunt bedenken die onder bepaalde omstandigheden optimaler is dan degene die de optimizer ondersteunt, kun je de optimizer niet verbeteren om deze te ondersteunen, en de optimizer kan niet leren om het te gebruiken. Wat u echter wel kunt doen, is de query herschrijven met behulp van alternatieve query-elementen die kunnen worden geoptimaliseerd met de strategie die u in gedachten heeft. In dit vijfde en laatste deel van de serie demonstreer ik deze techniek van het afstemmen van zoekopdrachten met behulp van queryrevisies.
Grote dank aan Paul White (@SQL_Kiwi) voor het helpen met enkele van de kostenberekeningen die in dit artikel worden gepresenteerd!
Net als in de vorige delen van de serie, zal ik de PerformanceV3-voorbeelddatabase gebruiken. Gebruik de volgende code om onnodige indexen uit de tabel Orders te verwijderen:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Standaard optimalisatiestrategie
Overweeg de volgende basisgroeperings- en aggregatietaken:
Retourneer de maximale besteldatum voor elke verzender, medewerker en klant.
Voor optimale prestaties maakt u de volgende ondersteunende indexen:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate); CREATE INDEX idx_eid_od ON dbo.Orders(empid, orderdate); CREATE INDEX idx_cid_od ON dbo.Orders(custid, orderdate);
Hieronder volgen de drie vragen die u zou gebruiken om deze taken uit te voeren, samen met de geschatte subboomkosten, evenals I/O-, CPU- en verstreken tijdstatistieken:
-- Query 1 -- Estimated Subtree Cost: 3.5344 -- logical reads: 2484, CPU time: 281 ms, elapsed time: 279 ms SELECT shipperid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY shipperid; -- Query 2 -- Estimated Subtree Cost: 3.62798 -- logical reads: 2610, CPU time: 250 ms, elapsed time: 283 ms SELECT empid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY empid; -- Query 3 -- Estimated Subtree Cost: 4.27624 -- logical reads: 3479, CPU time: 406 ms, elapsed time: 506 ms SELECT custid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY custid;
Afbeelding 1 toont de plannen voor deze zoekopdrachten:
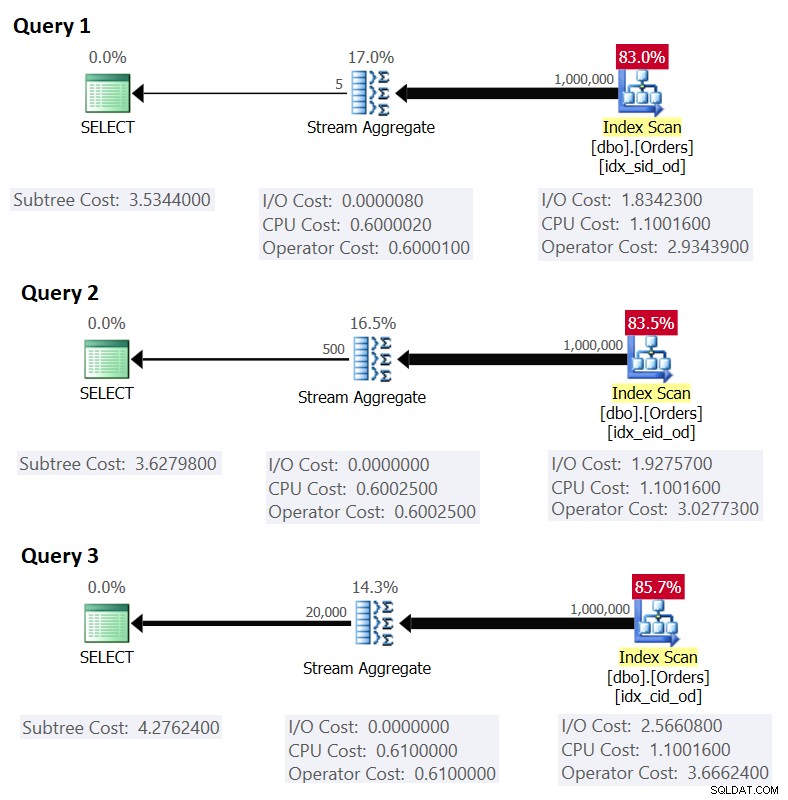Figuur 1:Plannen voor gegroepeerde zoekopdrachten
Bedenk dat als u een dekkingsindex hebt, met de kolommen van de groeperingsset als de belangrijkste sleutelkolommen, gevolgd door de aggregatiekolom, SQL Server waarschijnlijk een plan kiest dat een geordende scan uitvoert van de dekkingsindex die de Stream Aggregate-strategie ondersteunt . Zoals blijkt uit de plannen in figuur 1, is de Index Scan-operator verantwoordelijk voor het grootste deel van de plankosten, en daarbinnen is het I/O-gedeelte het meest prominent.
Voordat ik een alternatieve strategie presenteer en uitleg onder welke omstandigheden deze optimaal is dan de standaardstrategie, laten we eerst de kosten van de bestaande strategie evalueren. Aangezien het I/O-gedeelte het meest dominant is bij het bepalen van de plankosten van deze standaardstrategie, laten we eerst eens schatten hoeveel logische pagina's er nodig zijn om te lezen. Later zullen we ook de abonnementskosten schatten.
Om het aantal logische uitlezingen te schatten dat de Index Scan-operator nodig heeft, moet u weten hoeveel rijen u in de tabel heeft en hoeveel rijen op een pagina passen op basis van de rijgrootte. Zodra u deze twee operanden hebt, is uw formule voor het vereiste aantal pagina's op het bladniveau van de index CEILING(1e0 * @numrows / @rowsperpage). Als je alleen maar de tabelstructuur hebt en geen bestaande voorbeeldgegevens om mee te werken, kun je dit artikel gebruiken om het aantal pagina's te schatten dat je zou hebben op het bladniveau van de ondersteunende index. Als u over goede representatieve voorbeeldgegevens beschikt, zelfs als deze niet op dezelfde schaal zijn als in de productieomgeving, kunt u het gemiddelde aantal rijen dat op een pagina past, berekenen door catalogus- en dynamisch beheerobjecten op te vragen, zoals:
SELECT I.name, row_count, in_row_data_page_count,
CAST(ROUND(1e0 * row_count / in_row_data_page_count, 0) AS INT) AS avgrowsperpage
FROM sys.indexes AS I
INNER JOIN sys.dm_db_partition_stats AS P
ON I.object_id = P.object_id
AND I.index_id = P.index_id
WHERE I.object_id = OBJECT_ID('dbo.Orders')
AND I.name IN ('idx_sid_od', 'idx_eid_od', 'idx_cid_od'); Deze query genereert de volgende uitvoer in onze voorbeelddatabase:
name row_count in_row_data_page_count avgrowsperpage ----------- ---------- ---------------------- --------------- idx_sid_od 1000000 2473 404 idx_eid_od 1000000 2599 385 idx_cid_od 1000000 3461 289
Nu u het aantal rijen heeft dat in een leaf-pagina van de index past, kunt u het totale aantal leaf-pagina's in de index schatten op basis van het aantal rijen dat u van uw productietabel verwacht. Dit is ook het verwachte aantal logische uitlezingen dat door de Index Scan-operator moet worden toegepast. In de praktijk is er meer aan het aantal leesbewerkingen dat zou kunnen plaatsvinden dan alleen het aantal pagina's in het bladniveau van de index, zoals extra leesbewerkingen die worden geproduceerd door het vooruit lezen-mechanisme, maar ik zal die negeren om onze discussie eenvoudig te houden .
Het geschatte aantal logische leesbewerkingen voor Query 1 met betrekking tot het verwachte aantal rijen is bijvoorbeeld CEILING(1e0 * @numorws / 404). Met 1.000.000 rijen is het verwachte aantal logische leesbewerkingen 2476. Het verschil tussen 2476 en het gerapporteerde aantal rijen van 2473 kan worden toegeschreven aan de afronding die ik deed bij het berekenen van het gemiddelde aantal rijen per pagina.
Wat betreft de abonnementskosten, heb ik uitgelegd hoe u de kosten van de Stream Aggregate-operator kunt reverse-engineeren in deel 1 van de serie. Op een vergelijkbare manier kunt u de kosten van de Index Scan-operator reverse-engineeren. De plankosten zijn dan de som van de kosten van de Index Scan en Stream Aggregate operators.
Om de kosten van de Index Scan-operator te berekenen, moet u beginnen met reverse-engineering van enkele van de belangrijke constanten van het kostenmodel:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
Met de bovenstaande constanten van het kostenmodel berekend, kunt u doorgaan met het reverse engineeren van de formules voor de I/O-kosten, CPU-kosten en totale operatorkosten voor de Index Scan-operator:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.003125 + (@numpages - 1e0) * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011 Operator cost: 0.002541259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000011
De operatorkosten van de Index Scan voor Query 1, met 2473 pagina's en 1.000.000 rijen, zijn bijvoorbeeld:
0.002541259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000011 = 2.93439
Hieronder volgt de reverse-engineering formule voor de kosten van de Stream Aggregate-operator:
0.000008 + @numrows * 0.0000006 + @numgroups * 0.0000005
Voor Query 1 hebben we bijvoorbeeld 1.000.000 rijen en 5 groepen, vandaar dat de geschatte kosten 0,6000105 zijn.
Door de kosten van de twee operators te combineren, is hier de formule voor de volledige plankosten:
0.002549259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Voor Query 1, met 2473 pagina's, 1.000.000 rijen en 5 groepen, krijgt u:
0.002549259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5344
Dit komt overeen met wat in figuur 1 wordt weergegeven als de geschatte kosten voor query 1.
Als u zou uitgaan van een geschat aantal rijen per pagina, zou uw formule zijn:
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Voor Query 1 met 1.000.000 rijen, 404 rijen per pagina en 5 groepen zijn de geschatte kosten bijvoorbeeld:
0.002549259259259 + CEILING(1e0 * 1000000 / 404) * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5366
Als oefening kunt u de getallen voor Query 2 (1.000.000 rijen, 385 rijen per pagina, 500 groepen) en Query 3 (1.000.000 rijen, 289 rijen per pagina, 20.000 groepen) in onze formule toepassen en zien dat de resultaten overeenkomen met wat Figuur 1 toont.
Query-afstemming met herschrijving van query's
De standaard vooraf bestelde Stream Aggregate-strategie voor het berekenen van een MIN/MAX-aggregaat per groep is gebaseerd op een geordende scan van een ondersteunende dekkingsindex (of een andere voorbereidende activiteit die de geordende rijen uitzendt). Een alternatieve strategie, waarbij een ondersteunende dekkingsindex aanwezig is, zou zijn om per groep een indexzoektocht uit te voeren. Hier is een beschrijving van een pseudoplan op basis van een dergelijke strategie voor een zoekopdracht die is gegroepeerd op grpcol en een MAX(aggcol) toepast:
set @curgrpcol = grpcol from first row obtained by a scan of the index, ordered forward;
while end of index not reached
begin
set @curagg = aggcol from row obtained by a seek to the last point
where grpcol = @curgrpcol, ordered backward;
emit row (@curgrpcol, @curagg);
set @curgrpcol = grpcol from row to the right of last row for current group;
end; Als je erover nadenkt, is de standaard scangebaseerde strategie optimaal wanneer de groeperingsset een lage dichtheid heeft (groot aantal groepen, met gemiddeld een klein aantal rijen per groep). De op zoek gebaseerde strategie is optimaal wanneer de groeperingsset een hoge dichtheid heeft (klein aantal groepen, met gemiddeld een groot aantal rijen per groep). Afbeelding 2 illustreert beide strategieën die laten zien wanneer elk optimaal is.
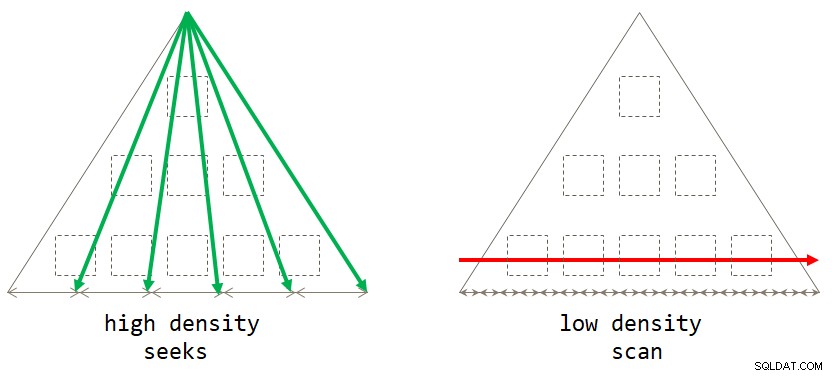Figuur 2:Optimale strategie gebaseerd op groeperingssetdichtheid
Zolang u de oplossing in de vorm van een gegroepeerde query schrijft, houdt SQL Server momenteel alleen rekening met de scanstrategie. Dit werkt goed voor u wanneer de groeperingsset een lage dichtheid heeft. Als u een hoge dichtheid heeft, moet u een herschrijving van de zoekopdracht toepassen om de zoekstrategie te krijgen. Een manier om dit te bereiken is om een query uit te voeren op de tabel die de groepen bevat, en om een scalaire statistische subquery te gebruiken tegen de hoofdtabel om de verzameling te verkrijgen. Om bijvoorbeeld de maximale besteldatum voor elke verzender te berekenen, gebruikt u de volgende code:
SELECT shipperid,
( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS maxod
FROM dbo.Shippers AS S; De indexeringsrichtlijnen voor de hoofdtabel zijn dezelfde als die ter ondersteuning van de standaardstrategie. We hebben die indexen al voor de drie bovengenoemde taken. U wilt waarschijnlijk ook een ondersteunende index op de kolommen van de groeperingsset in de tabel met de groepen om de I/O-kosten ten opzichte van die tabel te minimaliseren. Gebruik de volgende code om dergelijke ondersteunende indexen voor onze drie taken te maken:
CREATE INDEX idx_sid ON dbo.Shippers(shipperid); CREATE INDEX idx_eid ON dbo.Employees(empid); CREATE INDEX idx_cid ON dbo.Customers(custid);
Een klein probleem is echter dat de oplossing op basis van de subquery geen exact logisch equivalent is van de oplossing op basis van de gegroepeerde query. Als u een groep heeft zonder aanwezigheid in de hoofdtabel, zal de eerste de groep retourneren met een NULL als aggregaat, terwijl de laatste de groep helemaal niet retourneert. Een eenvoudige manier om een echt logisch equivalent van de gegroepeerde query te krijgen, is door de subquery aan te roepen met behulp van de CROSS APPLY-operator in de FROM-component in plaats van een scalaire subquery te gebruiken in de SELECT-component. Onthoud dat CROSS APPLY geen linkerrij retourneert als de toegepaste query een lege set retourneert. Hier zijn de drie oplossingsvragen die deze strategie voor onze drie taken implementeren, samen met hun prestatiestatistieken:
-- Query 4
-- Estimated Subtree Cost: 0.0072299
-- logical reads: 2 + 15, CPU time: 0 ms, elapsed time: 43 ms
SELECT S.shipperid, A.orderdate AS maxod
FROM dbo.Shippers AS S
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS A;
-- Query 5
-- Estimated Subtree Cost: 0.089694
-- logical reads: 2 + 1620, CPU time: 0 ms, elapsed time: 148 ms
SELECT E.empid, A.orderdate AS maxod
FROM dbo.Employees AS E
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.empid = E.empid
ORDER BY O.orderdate DESC ) AS A;
-- Query 6
-- Estimated Subtree Cost: 3.5227
-- logical reads: 45 + 63777, CPU time: 171 ms, elapsed time: 306 ms
SELECT C.custid, A.orderdate AS maxod
FROM dbo.Customers AS C
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.custid = C.custid
ORDER BY O.orderdate DESC ) AS A; De plannen voor deze zoekopdrachten worden weergegeven in figuur 3.
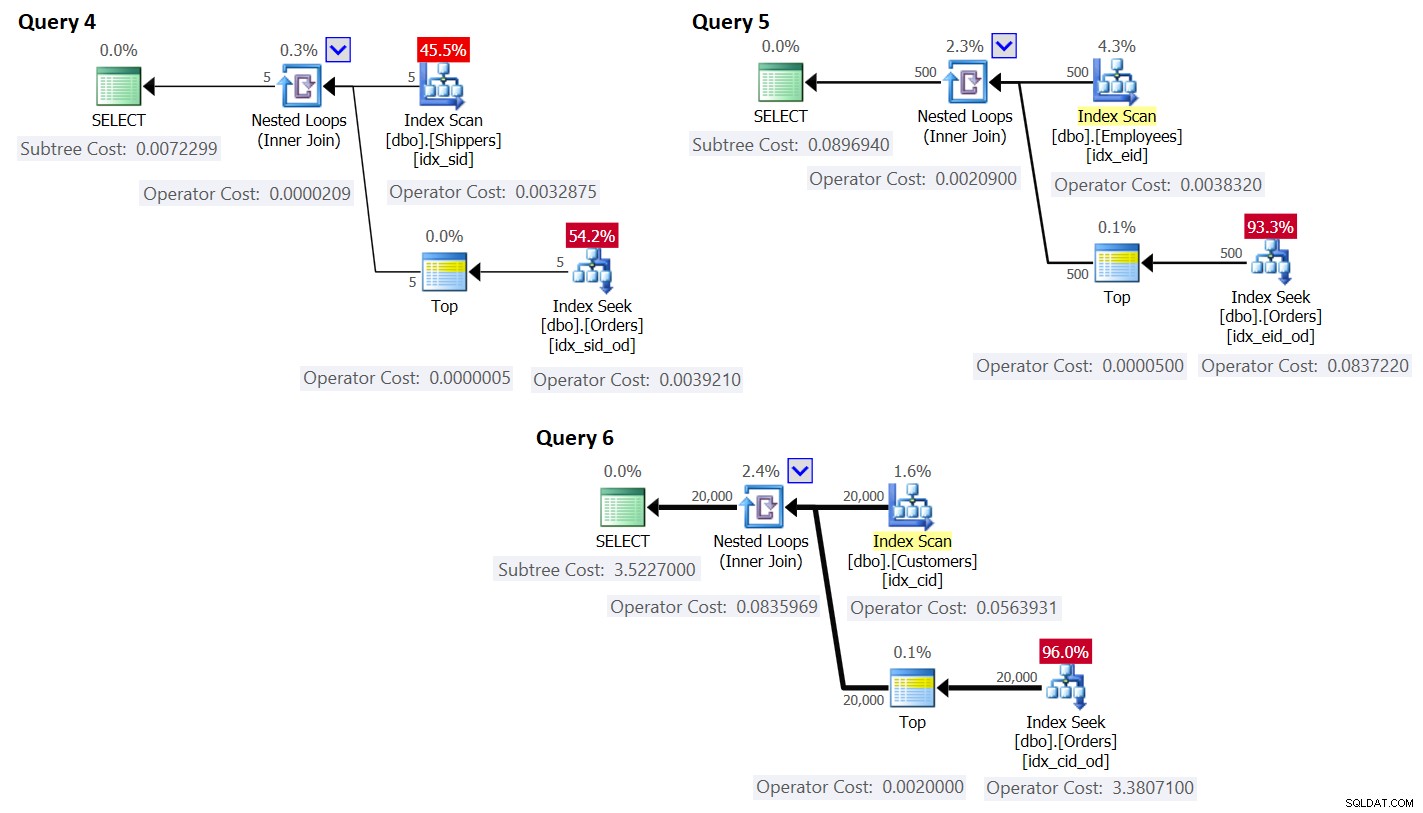Figuur 3:Plannen voor zoekopdrachten met herschrijven
Zoals u kunt zien, worden de groepen verkregen door de index op de groepstabel te scannen en het aggregaat wordt verkregen door een zoekopdracht in de index op de hoofdtabel toe te passen. Hoe hoger de dichtheid van de groeperingsset, hoe optimaler dit plan wordt vergeleken met de standaardstrategie voor de gegroepeerde zoekopdracht.
Laten we, net zoals we eerder deden voor de standaard scanstrategie, een schatting maken van het aantal logische leesbewerkingen en de kosten plannen voor de zoekstrategie. Het geschatte aantal logische reads is het aantal reads voor de enkele uitvoering van de Index Scan-operator die de groepen ophaalt, plus de reads voor alle uitvoeringen van de Index Seek-operator.
Het geschatte aantal logische uitlezingen voor de Index Scan-operator is verwaarloosbaar in vergelijking met de zoekopdrachten; toch is het PLAFOND (1e0 * @numgroups / @rowsperpage). Neem Query 4 als voorbeeld; stel dat de index idx_sid ongeveer 600 rijen per bladpagina past (het werkelijke aantal hangt af van de werkelijke shipperid-waarden aangezien het datatype VARCHAR(5) is). Met 5 groepen passen alle rijen in een enkele bladpagina. Als je 5.000 groepen had, zouden ze op 9 pagina's passen.
Het geschatte aantal logische leesbewerkingen voor alle uitvoeringen van de Index Seek-operator is @numgroups * @indexdepth. De diepte van de index kan worden berekend als:
CEILING(LOG(CEILING(1e0 * @numrows / @rowsperleafpage), @rowspernonleafpage)) + 1
Gebruik Query 4 als voorbeeld en stel dat we ongeveer 404 rijen per bladpagina van de index idx_sid_od kunnen plaatsen, en ongeveer 352 rijen per nietbladige pagina. Nogmaals, de werkelijke aantallen zijn afhankelijk van de werkelijke waarden die zijn opgeslagen in de kolom Shipperid, aangezien het datatype VARCHAR(5) is). Houd er voor schattingen rekening mee dat u de hier beschreven berekeningen kunt gebruiken. Als er goede representatieve voorbeeldgegevens beschikbaar zijn, kunt u de volgende query gebruiken om het aantal rijen te berekenen dat in de leaf- en nonleaf-pagina's van de gegeven index past:
SELECT
CASE P.index_level WHEN 0 THEN 'leaf' WHEN 1 THEN 'nonleaf' END AS pagetype,
FLOOR(8096 / (P.avg_record_size_in_bytes + 2)) AS rowsperpage
FROM (SELECT *
FROM sys.indexes
WHERE object_id = OBJECT_ID('dbo.Orders')
AND name = 'idx_sid_od') AS I
CROSS APPLY sys.dm_db_index_physical_stats
(DB_ID('PerformanceV3'), I.object_id, I.index_id, NULL, 'DETAILED') AS P
WHERE P.index_level <= 1; Ik kreeg de volgende uitvoer:
pagetype rowsperpage -------- ---------------------- leaf 404 nonleaf 352
Met deze getallen is de diepte van de index ten opzichte van het aantal rijen in de tabel:
CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1
Met 1.000.000 rijen in de tabel resulteert dit in een indexdiepte van 3. Bij ongeveer 50 miljoen rijen neemt de indexdiepte toe tot 4 niveaus en bij ongeveer 17,62 miljard rijen tot 5 niveaus.
In ieder geval, met betrekking tot het aantal groepen en het aantal rijen, uitgaande van het bovenstaande aantal rijen per pagina, berekent de volgende formule het geschatte aantal logische leesbewerkingen voor Query 4:
CEILING(1e0 * @numgroups / 600) + @numgroups * (CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1)
Met bijvoorbeeld 5 groepen en 1.000.000 rijen krijgt u in totaal slechts 16 reads! Bedenk dat de standaard scangebaseerde strategie voor de gegroepeerde query evenveel logische leesbewerkingen omvat als CEILING(1e0 * @numrows / @rowsperpage). Als u Query 1 als voorbeeld gebruikt, en uitgaande van ongeveer 404 rijen per bladpagina van de index idx_sid_od, met hetzelfde aantal rijen van 1.000.000, krijgt u ongeveer 2.476 reads. Verhoog het aantal rijen in de tabel met een factor 1.000 tot 1.000.000.000, maar houd het aantal groepen vast. Het aantal leesbewerkingen dat nodig is met de zoekstrategie verandert heel weinig tot 21, terwijl het aantal leesbewerkingen dat nodig is met de scanstrategie lineair toeneemt tot 2.475.248.
Het mooie van de seeks-strategie is dat zolang het aantal groepen klein en vast is, het bijna constant wordt geschaald met betrekking tot het aantal rijen in de tabel. Dat komt omdat het aantal zoekacties wordt bepaald door het aantal groepen, en de diepte van de index heeft betrekking op het aantal rijen in de tabel op een logaritmische manier, waarbij de logbasis het aantal rijen is dat op een niet-bladige pagina past. Omgekeerd heeft de scangebaseerde strategie een lineaire schaal met betrekking tot het aantal betrokken rijen.
Afbeelding 4 toont het geschatte aantal reads voor de twee strategieën, toegepast door Query 1 en Query 4, gegeven een vast aantal groepen van 5 en verschillende aantallen rijen in de hoofdtabel.
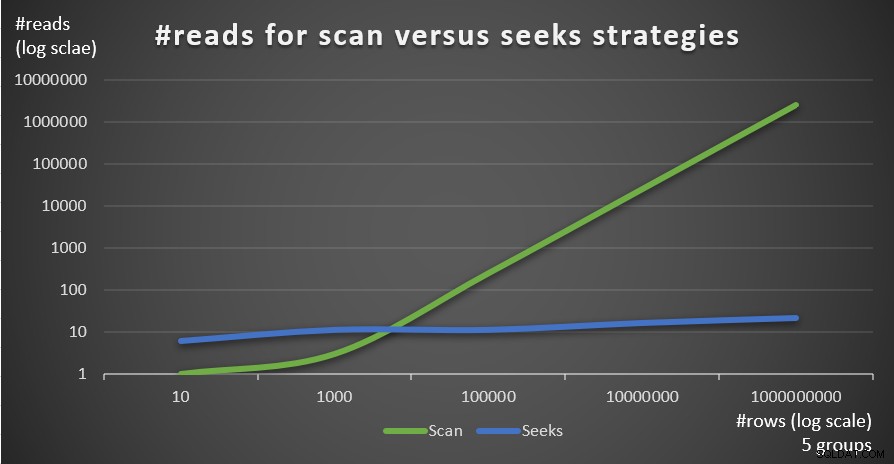Figuur 4:#reads voor scan versus zoekt strategieën (5 groepen)
Afbeelding 5 toont het geschatte aantal leesbewerkingen voor de twee strategieën, gegeven een vast aantal rijen van 1.000.000 in de hoofdtabel en verschillende aantallen groepen.
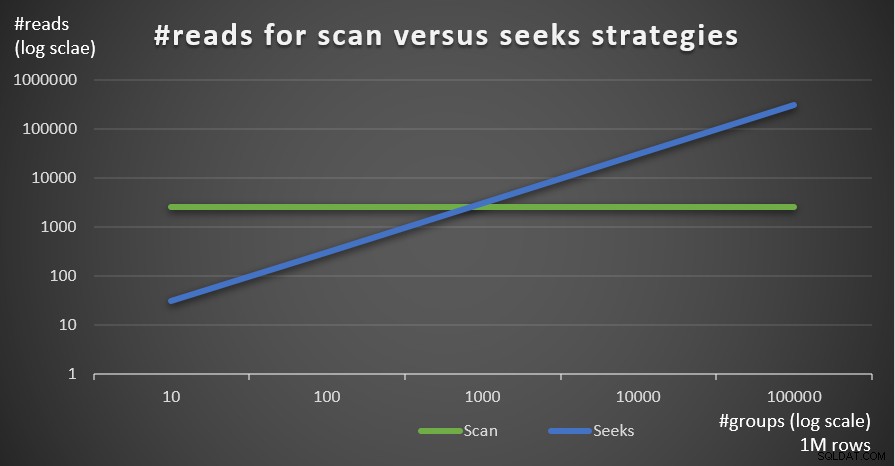Figuur 5:#reads voor scan- versus zoekstrategieën (1 miljoen rijen)
Je kunt heel duidelijk zien dat hoe hoger de dichtheid van de groeperingsset (kleiner aantal groepen) en hoe groter de hoofdtabel, hoe meer de voorkeur wordt gegeven aan de seeks-strategie in termen van het aantal reads. Als u zich afvraagt welk I/O-patroon door elke strategie wordt gebruikt; inderdaad, indexzoekbewerkingen voeren willekeurige I/O uit, terwijl een indexscanbewerking sequentiële I/O uitvoert. Toch is het vrij duidelijk welke strategie in de meer extreme gevallen het meest optimaal is.
Wat betreft de kosten van het queryplan, nogmaals, met het plan voor Query 4 in Afbeelding 3 als voorbeeld, laten we het uitsplitsen naar de individuele operators in het plan.
De reverse-engineered formule voor de kosten van de Index Scan-operator is:
0.002541259259259 + @numpages * 0.000740740740741 + @numgroups * 0.0000011
In ons geval, met 5 groepen, die allemaal op één pagina passen, zijn de kosten:
0.002541259259259 + 1 * 0.000740740740741 + 5 * 0.0000011 = 0.0032875
De kosten die in het abonnement worden weergegeven, zijn hetzelfde.
Zoals eerder zou je het aantal pagina's in het bladniveau van de index kunnen schatten op basis van het geschatte aantal rijen per pagina met behulp van de formule CEILING(1e0 * @numrows / @rowsperpage), wat in ons geval CEILING(1e0 * @ is). numgroups / @groupsperpage). Stel dat de index idx_sid ongeveer 600 rijen per bladpagina past, met 5 groepen zou je één pagina moeten lezen. In ieder geval wordt de calculatieformule voor de Index Scan operator dan:
0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage) * 0.000740740740741 + @numgroups * 0.0000011
De reverse engineered costing-formule voor de Nested Loops-operator is:
@executions * 0.00000418
In ons geval vertaalt dit zich naar:
@numgroups * 0.00000418
Voor Query 4, met 5 groepen, krijg je:
5 * 0.00000418 = 0.0000209
De kosten die in het abonnement worden weergegeven, zijn hetzelfde.
De reverse engineered costing-formule voor de Top-operator is:
@executions * @toprows * 0.00000001
In ons geval vertaalt dit zich naar:
@numgroups * 1 * 0.00000001
Met 5 groepen krijg je:
5 * 0.0000001 = 0.0000005
De kosten die in het abonnement worden weergegeven, zijn hetzelfde.
Wat betreft de Index Seek-operator, hier kreeg ik geweldige hulp van Paul White; bedankt, mijn vriend! De berekening is anders voor de eerste uitvoering en voor de rebinds (niet-eerste uitvoeringen die het resultaat van de vorige uitvoering niet hergebruiken). Laten we, net als bij de Index Scan-operator, beginnen met het identificeren van de constanten van het kostenmodel:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
Voor één uitvoering, zonder toepassing van een rijdoel, zijn de I/O- en CPU-kosten:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.002384259259259 + @numpages * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011
Omdat we TOP (1) gebruiken, hebben we maar één pagina en één rij nodig, dus de kosten zijn:
I/O cost: 0.002384259259259 + 1 * 0.000740740740741 = 0.003125 CPU cost: 0.000157 + 1 * 0.0000011 = 0.0001581
Dus de kosten van de eerste uitvoering van de Index Seek-operator zijn in ons geval:
@firstexecution = 0.003125 + 0.0001581 = 0.0032831
Wat betreft de kosten van de rebinds, deze zijn zoals gewoonlijk gemaakt van CPU- en I/O-kosten. Laten we ze respectievelijk @rebindcpu en @rebindio noemen. Met Query 4, met 5 groepen, hebben we 4 rebinds (noem het @rebinds). De kosten van @rebindcpu zijn het makkelijke gedeelte. De formule is:
@rebindcpu = @rebinds * (@cpubase + @cpurow)
In ons geval vertaalt dit zich naar:
@rebindcpu = 4 * (0.000157 + 0.0000011) = 0.0006324
Het @rebindio-gedeelte is iets complexer. Hier berekent de kostprijsformule, statistisch gezien, het verwachte aantal afzonderlijke pagina's dat de rebinds naar verwachting zullen lezen met behulp van steekproeven met vervanging. We noemen dit element @pswr (voor verschillende pagina's die zijn gesampled met vervanging). Het idee is dat we @indexdatapages aantal pagina's in de index hebben (in ons geval 2.473), en @rebinds aantal rebinds (in ons geval 4). Ervan uitgaande dat we dezelfde kans hebben om een bepaalde pagina te lezen bij elke nieuwe binding, hoeveel afzonderlijke pagina's worden dan in totaal verwacht te lezen? Dit is vergelijkbaar met het hebben van een zak met 2473 ballen, en vier keer blindelings een bal uit de zak trekken en deze dan terug in de zak doen. Hoeveel verschillende ballen moet je statistisch gezien in totaal trekken? De formule hiervoor, met behulp van onze operanden, is:
@pswr = @indexdatapages * (1e0 - POWER((@indexdatapages - 1e0) / @indexdatapages, @rebinds))
Met onze nummers krijg je:
@pswr = 2473 * (1e0 - POWER((2473 - 1e0) / 2473, 4)) = 3.99757445099277
Vervolgens bereken je het aantal rijen en pagina's dat je gemiddeld per groep hebt:
@grouprows = @cardinality * @density @grouppages = CEILING(@indexdatapages * @density)
In onze Query 4 is de kardinaliteit 1.000.000 en is de dichtheid 1/5 =0,2. Dus je krijgt:
@grouprows = 1000000 * 0.2 = 200000 @numpages = CEILING(2473 * 0.2) = 495
Vervolgens bereken je de I/O-kosten zonder te filteren (noem het @io) als:
@io = @randomio + (@seqio * (@grouppages - 1e0))
In ons geval krijg je:
@io = 0.003125 + (0.000740740740741 * (495 - 1e0)) = 0.369050925926054
En tot slot, aangezien de seek slechts één rij extraheert in elke rebind, bereken je @rebindio met de volgende formule:
@rebindio = (1e0 / @grouprows) * ((@pswr - 1e0) * @io)
In ons geval krijg je:
@rebindio = (1e0 / 200000) * ((3.99757445099277 - 1e0) * 0.369050925926054) = 0.000005531288
Ten slotte zijn de kosten van de operator:
Operator cost: @firstexecution + @rebindcpu + @rebindio = 0.0032831 + 0.0006324 + 0.000005531288 = 0.003921031288
Dit is hetzelfde als de kosten van de Index Seek-operator die worden weergegeven in het plan voor Query 4.
U kunt nu de kosten van alle operators samenvoegen om de volledige kosten van het queryplan te krijgen. Je krijgt:
KostenQuery plan cost: 0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00000418
+ @numgroups * 0.00000001
+ 0.0032831 + (@numgroups - 1e0) * 0.0001581
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0))) Na vereenvoudiging krijgt u de volgende volledige kostprijsformule voor onze Seeks-strategie:
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0))) Als voorbeeld, met behulp van T-SQL, hier is de berekening van de kosten van het queryplan met onze Seeks-strategie voor Query 4:
DECLARE
@numrows AS FLOAT = 1000000,
@numgroups AS FLOAT = 5,
@rowsperpage AS FLOAT = 404,
@groupsperpage AS FLOAT = 600;
SELECT
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0)))
AS seeksplancost; Deze berekening berekent de kosten 0,0072295 voor Query 4. De geschatte kosten die worden weergegeven in Afbeelding 3 zijn 0,0072299. Dat is best dichtbij! Bereken bij wijze van oefening de kosten voor Query 5 en Query 6 met behulp van deze formule en controleer of u getallen krijgt die in de buurt komen van die in Afbeelding 3.
Bedenk dat de kostenformule voor de standaard scangebaseerde strategie is (noem het Scan strategie):
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Als u Query 1 als voorbeeld gebruikt en uitgaande van 1.000.000 rijen in de tabel, 404 rijen per pagina en 5 groepen, bedragen de geschatte kosten van het queryplan van de scanstrategie 3,5366.
Afbeelding 6 toont de geschatte kosten van het queryplan voor de twee strategieën, toegepast door Query 1 (scan) en Query 4 (zoekt), gegeven een vast aantal groepen van 5 en verschillende aantallen rijen in de hoofdtabel.
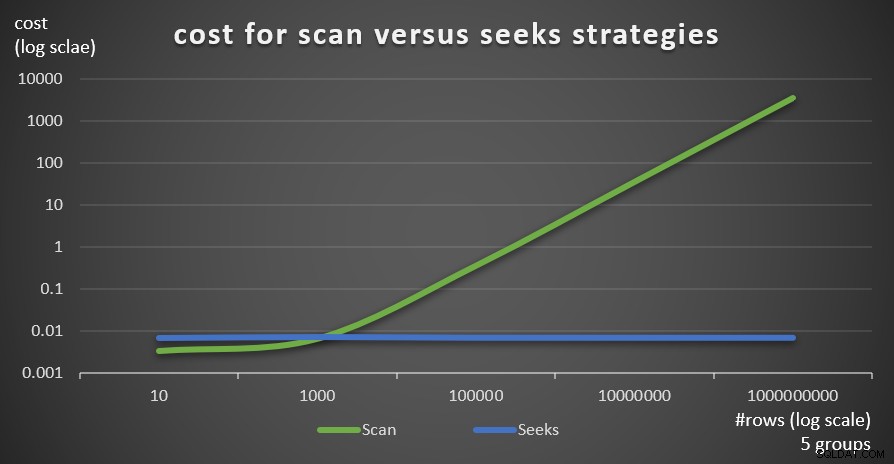Figuur 6:kosten voor scan versus zoekt strategieën (5 groepen)
Afbeelding 7 toont de geschatte kosten van het queryplan voor de twee strategieën, gegeven een vast aantal rijen in de hoofdtabel van 1.000.000, en verschillende aantallen groepen.
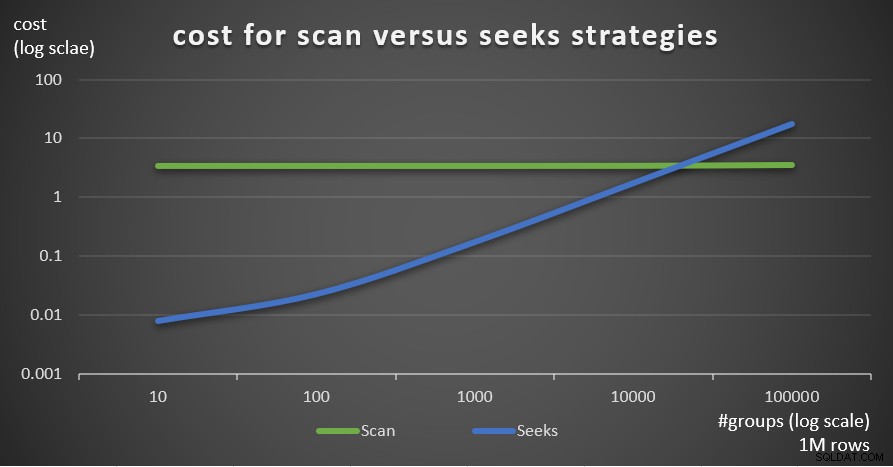Figuur 7:kosten voor scan versus zoekt strategieën (1 miljoen rijen)
Zoals uit deze bevindingen blijkt, geldt dat hoe hoger de dichtheid van de groeperingsset en hoe meer rijen in de hoofdtabel, hoe optimaal de zoekstrategie wordt vergeleken met de scanstrategie. Zorg er dus voor dat u in scenario's met hoge dichtheid de op APPLY gebaseerde oplossing probeert. Ondertussen kunnen we hopen dat Microsoft deze strategie zal toevoegen als een ingebouwde optie voor gegroepeerde zoekopdrachten.
Conclusie
Dit artikel sluit een vijfdelige serie af over drempelwaarden voor query-optimalisatie voor query's die gegevens groeperen en verzamelen. Een doel van de serie was het bespreken van de specifieke kenmerken van de verschillende algoritmen die de optimizer kan gebruiken, de voorwaarden waaronder elk algoritme de voorkeur heeft en wanneer u moet ingrijpen bij het herschrijven van uw eigen query. Een ander doel was om het proces van het ontdekken van de verschillende opties en het vergelijken ervan uit te leggen. Het is duidelijk dat hetzelfde analyseproces kan worden toegepast op filteren, samenvoegen, vensters en vele andere aspecten van query-optimalisatie. Hopelijk voel je je nu beter uitgerust om met het afstemmen van zoekopdrachten om te gaan dan voorheen.