Uitdagingsoplossingen voor generatorreeksen - deel 4

Dit is het vierde deel in een serie over oplossingen voor de uitdaging voor het genereren van getallenreeksen. Veel dank aan Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea en Paul White voor het delen van uw ideeën en opmerkingen.

Ik hou van het werk van Paul White. Ik blijf geschokt door zijn ontdekkingen en vraag me af hoe hij erachter komt wat hij doet. Ik hou ook van zijn efficiënte en welsprekende schrijfstijl. Vaak schud ik tijdens het lezen van zijn artikelen of posts mijn hoofd en vertel ik mijn vrouw, Lilach, dat ik als ik groot ben, net als Paul wil zijn.

Toen ik de uitdaging oorspronkelijk plaatste, hoopte ik stiekem dat Paul een oplossing zou posten. Ik wist dat als hij dat deed, het een heel speciale zou zijn. Nou, dat deed hij, en het is fascinerend! Het heeft uitstekende prestaties en er is nogal wat dat je ervan kunt leren. Dit artikel is gewijd aan de oplossing van Paul.

Ik doe mijn tests in tempdb, waardoor I/O- en tijdstatistieken worden ingeschakeld:

SET NOCOUNT ON;
 
USE tempdb;
 
SET STATISTICS TIME, IO ON;

Beperkingen van eerdere ideeën

Bij het evalueren van eerdere oplossingen, was een van de belangrijke factoren voor het verkrijgen van goede prestaties de mogelijkheid om batchverwerking toe te passen. Maar hebben we er maximaal gebruik van gemaakt?

Laten we eens kijken naar de plannen voor twee van de eerdere oplossingen die batchverwerking gebruikten. In deel 1 heb ik de functie dbo.GetNumsAlanCharlieItzikBatch behandeld, die ideeën van Alan, Charlie en mijzelf combineerde.

Dit is de definitie van de functie:

-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO
 
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
 
-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
 
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Deze oplossing definieert een basistabelwaarde-constructor met 16 rijen en een reeks trapsgewijze CTE's met kruiskoppelingen om het aantal rijen op te drijven tot mogelijk 4B. De oplossing gebruikt de functie ROW_NUMBER om de basisreeks van getallen te maken in een CTE met de naam Nums, en het TOP-filter om de gewenste kardinaliteit van de nummerreeks te filteren. Om batchverwerking mogelijk te maken, gebruikt de oplossing een dummy left join met een false voorwaarde tussen de Nums CTE en een tabel met de naam dbo.BatchMe, die een columnstore-index heeft.

Gebruik de volgende code om de functie te testen met de variabele toewijzingstechniek:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

De Plan Explorer-afbeelding van de werkelijke plan voor deze uitvoering wordt getoond in figuur 1.

Figuur 1:Plan voor dbo.GetNumsAlanCharlieItzikBatch-functie

Bij het analyseren van batchmodus versus rijmodusverwerking, is het best leuk om te kunnen zien door alleen naar een plan op een hoog niveau te kijken welke verwerkingsmodus elke operator gebruikte. Inderdaad, Plan Explorer toont een lichtblauw batchcijfer linksonder in de operator wanneer de daadwerkelijke uitvoeringsmodus Batch is. Zoals u in afbeelding 1 kunt zien, is de enige operator die de batchmodus heeft gebruikt de Window Aggregate-operator, die de rijnummers berekent. Er is nog veel werk gedaan door andere operators in de rijmodus.

Dit zijn de prestatiecijfers die ik in mijn test heb gekregen:

logische leest 0

Gebruik de optie Actual Execution Plan in SSMS of de Get Actual Plan-optie in Plan Explorer om te bepalen welke operators de meeste tijd nodig hadden om uit te voeren. Zorg ervoor dat je het recente artikel van Paul, Understanding Execution Plan Operator Timings, leest. Het artikel beschrijft hoe de gerapporteerde uitvoeringstijden van de operators kunnen worden genormaliseerd om de juiste cijfers te krijgen.

In het plan in figuur 1 wordt de meeste tijd besteed door de meest linkse geneste lussen en top-operators, die beide in rijmodus werken. Behalve dat rijmodus minder efficiënt is dan batchmodus voor CPU-intensieve bewerkingen, moet u er ook rekening mee houden dat het overschakelen van rij- naar batchmodus en terug extra tol vraagt.

In deel 2 heb ik een andere oplossing behandeld die batchverwerking gebruikte, geïmplementeerd in de functie dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. Deze oplossing combineerde ideeën van John Number2, Dave Mason, Joe Obbish, Alan, Charlie en mijzelf. Het belangrijkste verschil tussen de vorige oplossing en deze is dat de eerste als basiseenheid een virtuele tabelwaarde-constructor gebruikt en de laatste een echte tabel met een columnstore-index, waardoor u batchverwerking "gratis" krijgt. Dit is de code die de tabel maakt en deze vult met behulp van een INSERT-instructie met 102.400 rijen om deze te laten comprimeren:

DROP TABLE IF EXISTS dbo.NullBits102400;
GO
 
CREATE TABLE dbo.NullBits102400
(
  b BIT NULL, 
  INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
    WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
 
WITH
  L0 AS (SELECT CAST(NULL AS BIT) AS b
         FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
  L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
  nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b) 
  SELECT TOP(102400) b FROM nulls;
GO

Dit is de definitie van de functie:

CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
  (@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
  WITH
    Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
             FROM dbo.NullBits102400 AS A
               CROSS JOIN dbo.NullBits102400 AS B)
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums
  ORDER BY rownum;
GO

Een enkele kruisverbinding tussen twee instanties van de basistabel is voldoende om veel meer te produceren dan het gewenste potentieel van 4B-rijen. Ook hier gebruikt de oplossing de functie ROW_NUMBER om de basisreeks van getallen te produceren en het TOP-filter om de gewenste kardinaliteit van de getallenreeks te beperken.

Hier is de code om de functie te testen met behulp van de variabele toewijzingstechniek:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

Het plan voor deze uitvoering is weergegeven in figuur 2.

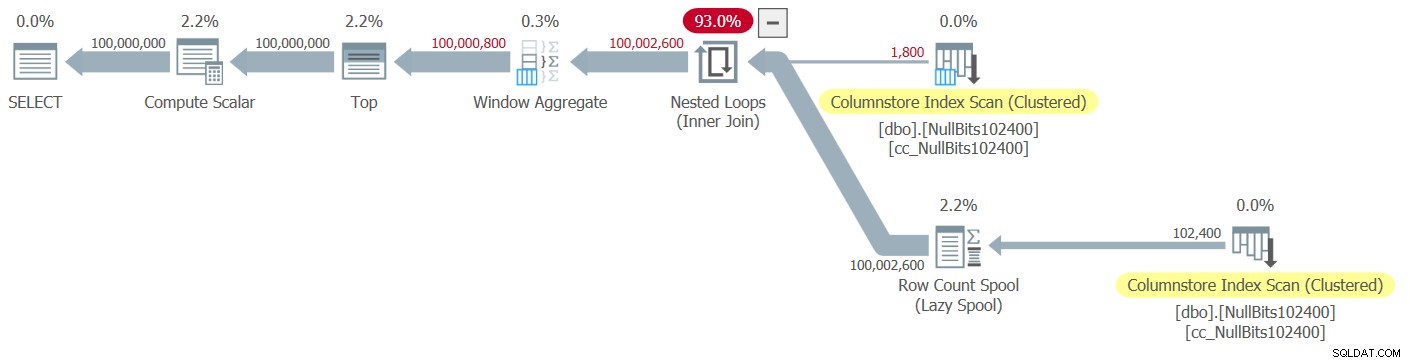Figuur 2:Plan voor de functie dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2

Merk op dat slechts twee operators in dit plan de batchmodus gebruiken:de bovenste scan van de geclusterde columnstore-index van de tabel, die wordt gebruikt als de buitenste invoer van de Nested Loops-join, en de Window Aggregate-operator, die wordt gebruikt om de basisrijnummers te berekenen .

Ik heb de volgende prestatiecijfers voor mijn test:

Tabel 'NullBits102400'. Aantal scans 2, logische waarden 0, fysieke waarden 0, paginaserver leest 0, read-ahead leest 0, pageserver read-ahead leest 0, lob logische leest 8, lob fysieke leest 0, lob pageserver leest 0, lob read- vooruit leest 0, lob page server read-ahead leest 0.

Tabel 'NullBits102400'. Segment leest 2, segment slaat 0 over.

Nogmaals, de meeste tijd in de uitvoering van dit plan wordt besteed door de meest linkse Geneste Loops en Top-operators, die in rijmodus worden uitgevoerd.

Pauls oplossing

Voordat ik Pauls oplossing presenteer, zal ik beginnen met mijn theorie over het denkproces dat hij doormaakte. Dit is eigenlijk een geweldige leeroefening en ik stel voor dat u deze doorneemt voordat u naar de oplossing kijkt. Paul herkende de slopende effecten van een plan dat zowel batch- als row-modi combineert, en daagde zichzelf uit om met een oplossing te komen die een all-batch-modusplan krijgt. Indien succesvol, is het potentieel voor een dergelijke oplossing om goed te presteren vrij groot. Het is zeker intrigerend om te zien of een dergelijk doel zelfs haalbaar is, aangezien er nog steeds veel operators zijn die de batchmodus nog niet ondersteunen en veel factoren die batchverwerking belemmeren. Op het moment van schrijven is het enige join-algoritme dat batchverwerking ondersteunt bijvoorbeeld het hash-join-algoritme. Een cross join wordt geoptimaliseerd met behulp van het geneste lussen-algoritme. Bovendien is de operator Top momenteel alleen in rijmodus geïmplementeerd. Deze twee elementen zijn cruciale fundamentele elementen die worden gebruikt in de plannen voor veel van de oplossingen die ik tot nu toe heb behandeld, inclusief de twee bovenstaande.

Ervan uitgaande dat je de uitdaging hebt gegeven om een ​​oplossing te creëren met een volledig batch-modusplan, gaan we verder met de tweede oefening. Ik zal eerst de oplossing van Paul presenteren zoals hij die heeft gegeven, met zijn inline opmerkingen. Ik zal het ook uitvoeren om de prestaties te vergelijken met de andere oplossingen. Ik heb veel geleerd door zijn oplossing stap voor stap te deconstrueren en te reconstrueren, om er zeker van te zijn dat ik goed begreep waarom hij elk van de technieken die hij deed gebruikte. Ik stel voor dat je hetzelfde doet voordat je verder gaat met het lezen van mijn uitleg.

Hier is de oplossing van Paul, die een helper columnstore-tabel met de naam dbo.CS en een functie met de naam dbo.GetNums_SQLkiwi omvat:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO
 
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
        @low - 2 + N.rn < @high;
GO

Hier is de code die ik heb gebruikt om de functie te testen met de variabele toewijzingstechniek:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ik heb het plan dat in figuur 3 wordt getoond voor mijn test.

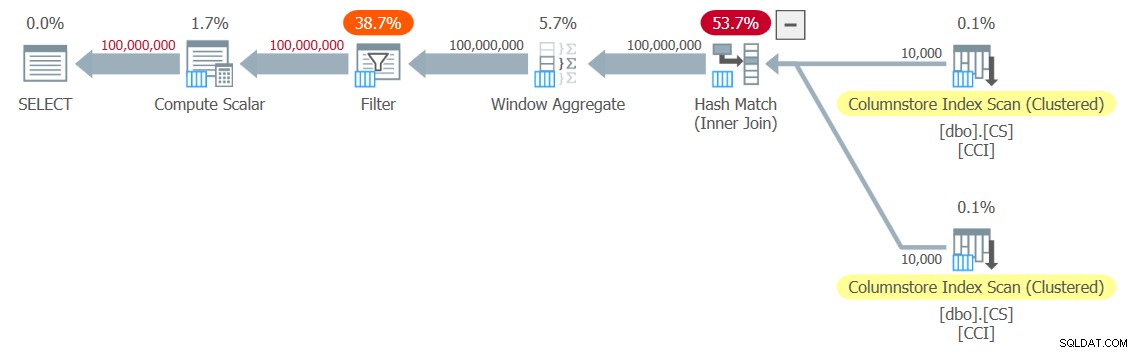Figuur 3:Plan voor de functie dbo.GetNums_SQLkiwi

Het is een all-batch-modus plan! Dat is behoorlijk indrukwekkend.

Dit zijn de prestatiecijfers die ik voor deze test op mijn machine heb gekregen:

Tabel 'CS'. Aantal scans 2, logische waarden 0, fysieke waarden 0, paginaserver leest 0, read-ahead leest 0, pageserver read-ahead leest 0, lob logische leest 44, lob fysieke leest 0, lob pageserver leest 0, lob read- vooruit leest 0, lob page server read-ahead leest 0.

Tabel 'CS'. Segment leest 2, segment slaat 0 over.

Laten we ook verifiëren dat als je de getallen moet retourneren die zijn geordend op n, de oplossing de volgorde behoudt met betrekking tot rn - tenminste als je constanten als invoer gebruikt - en dus expliciete sortering in het plan te vermijden. Hier is de code om het met bestelling te testen:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;

U krijgt hetzelfde abonnement als in figuur 3, en dus vergelijkbare prestatiecijfers:

Tabel 'CS'. Aantal scans 2, logische waarden 0, fysieke waarden 0, paginaserver leest 0, read-ahead leest 0, pageserver read-ahead leest 0, lob logische leest 44, lob fysieke leest 0, lob pageserver leest 0, lob read- vooruit leest 0, lob page server read-ahead leest 0.

Tabel 'CS'. Segment leest 2, segment slaat 0 over.

Dat is een belangrijke kant van de oplossing.

Onze testmethodologie wijzigen

De prestaties van Paul's oplossing zijn een behoorlijke verbetering in zowel de verstreken tijd als de CPU-tijd in vergelijking met de twee vorige oplossingen, maar het lijkt niet de meer dramatische verbetering die je zou verwachten van een plan met alle batchmodi. Misschien missen we iets?

Laten we proberen de uitvoeringstijden van de operator te analyseren door te kijken naar het werkelijke uitvoeringsplan in SSMS, zoals weergegeven in figuur 4.

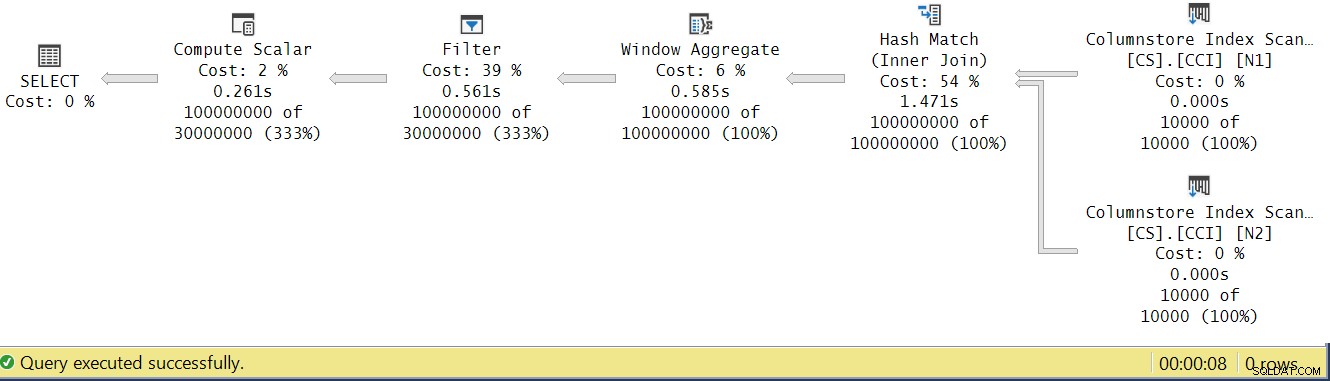Figuur 4:Uitvoeringstijden operator voor de functie dbo.GetNums_SQLkiwi

In het artikel van Paul over het analyseren van de uitvoeringstijden van operators legt hij uit dat operators in batchmodus elk hun eigen uitvoeringstijd rapporteren. Als je de uitvoeringstijden van alle operators in dit eigenlijke plan optelt, krijg je 2,878 seconden, maar het plan kostte 7,876 om uit te voeren. 5 seconden van de uitvoeringstijd lijken te ontbreken. Het antwoord hierop ligt in de testtechniek die we gebruiken, met de variabele toewijzing. Bedenk dat we besloten hebben om deze techniek te gebruiken om de noodzaak te elimineren om alle rijen van de server naar de beller te sturen en om de I/O's te vermijden die betrokken zouden zijn bij het schrijven van het resultaat naar een tabel. Het leek de perfecte optie. De werkelijke kosten van de variabele toewijzing zijn echter verborgen in dit plan, en het wordt natuurlijk uitgevoerd in rijmodus. Mysterie opgelost.

Uiteraard is een goede test uiteindelijk een test die uw productiegebruik van de oplossing adequaat weergeeft. Als u de gegevens doorgaans naar een tabel schrijft, moet uw test dat weergeven. Als u het resultaat naar de beller stuurt, heeft u uw test nodig om dat weer te geven. In ieder geval lijkt de variabele toewijzing een groot deel van de uitvoeringstijd in onze test te vertegenwoordigen, en het is duidelijk onwaarschijnlijk dat dit typisch productiegebruik van de functie vertegenwoordigt. Paul suggereerde dat in plaats van variabele toewijzing de test een eenvoudig aggregaat zoals MAX zou kunnen toepassen op de geretourneerde nummerkolom (n/rn/op). Een aggregaatoperator kan batchverwerking gebruiken, dus het plan omvat geen conversie van batch- naar rijmodus als gevolg van het gebruik ervan, en de bijdrage aan de totale looptijd moet vrij klein en bekend zijn.

Laten we dus alle drie de oplossingen die in dit artikel worden behandeld, opnieuw testen. Hier is de code om de functie dbo te testen.GetNumsAlanCharlieItzikBatch:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Ik heb het plan dat in figuur 5 wordt getoond voor deze test.

Figuur 5:Plan voor dbo.GetNumsAlanCharlieItzikBatch-functie met aggregaat

Dit zijn de prestatiecijfers die ik voor deze test heb gekregen:

logische leest 0

Merk op dat de runtime daalde van 10,025 seconden met behulp van de variabele toewijzingstechniek tot 8,733 met behulp van de aggregatietechniek. Dat is iets meer dan een seconde uitvoeringstijd die we kunnen toeschrijven aan de variabele toewijzing hier.

Hier is de code om de functie dbo te testen.GetNumsJohn2DaveObbishAlanCharlieItzik2:

SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

Ik heb het plan dat in figuur 6 wordt getoond voor deze test.

Figuur 6:Plan voor dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 functie met aggregaat

Dit zijn de prestatiecijfers die ik voor deze test heb gekregen:

Tabel 'NullBits102400'. Aantal scans 2, logische waarden 0, fysieke waarden 0, paginaserver leest 0, read-ahead leest 0, pageserver read-ahead leest 0, lob logische leest 8, lob fysieke leest 0, lob pageserver leest 0, lob read- vooruit leest 0, lob page server read-ahead leest 0.

Tabel 'NullBits102400'. Segment leest 2, segment slaat 0 over.

Merk op dat de runtime daalde van 9,813 seconden met behulp van de variabele toewijzingstechniek naar 7,053 met behulp van de aggregatietechniek. Dat is iets meer dan twee seconden uitvoeringstijd die we kunnen toeschrijven aan de variabele toewijzing hier.

En hier is de code om de oplossing van Paul te testen:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

Ik krijg het plan weergegeven in figuur 7 voor deze test.

Figuur 7:Plan voor dbo.GetNums_SQLkiwi-functie met aggregaat

En nu het grote moment. Ik heb de volgende prestatiecijfers voor deze test:

Tabel 'CS'. Aantal scans 2, logische waarden 0, fysieke waarden 0, paginaserver leest 0, read-ahead leest 0, pageserver read-ahead leest 0, lob logische leest 44, lob fysieke leest 0, lob pageserver leest 0, lob read- vooruit leest 0, lob page server read-ahead leest 0.

Tabel 'CS'. Segment leest 2, segment slaat 0 over.

De looptijd is gedaald van 7,822 seconden naar 3,149 seconden! Laten we eens kijken naar de uitvoeringstijden van de operator in het eigenlijke plan in SSMS, zoals weergegeven in figuur 8.

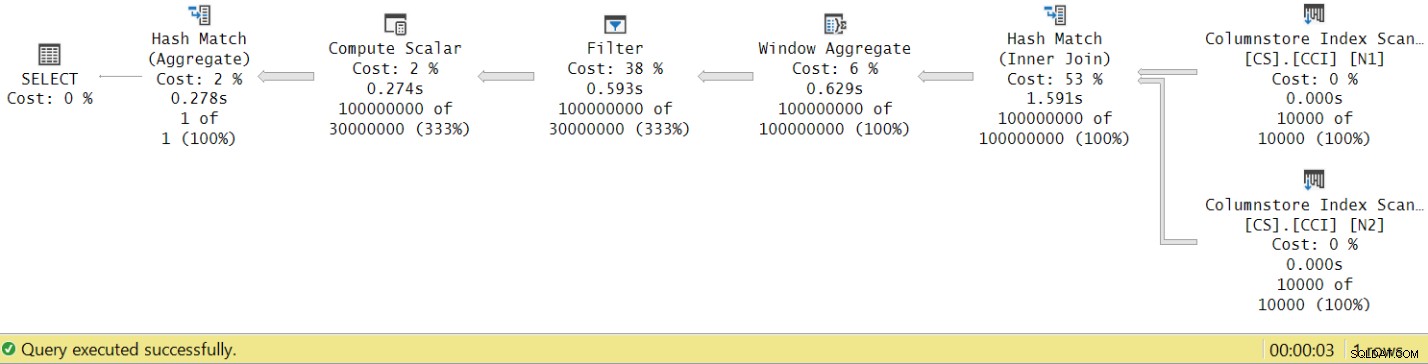Figuur 8:Uitvoeringstijden operator voor dbo.GetNums-functie met aggregaat

Als u nu de uitvoeringstijden van de individuele operators optelt, krijgt u een gelijkaardig aantal als de totale uitvoeringstijd van het plan.

Afbeelding 9 toont een prestatievergelijking in termen van verstreken tijd tussen de drie oplossingen met behulp van zowel de variabele toewijzing als de geaggregeerde testtechnieken.

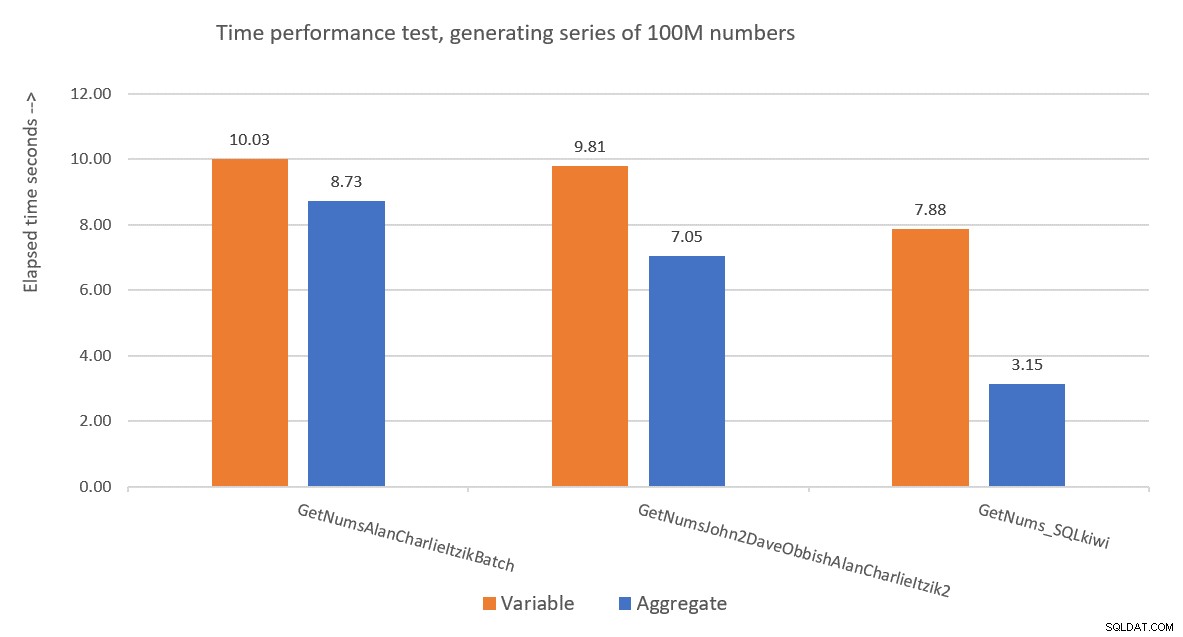Figuur 9:Prestatievergelijking

De oplossing van Paul is een duidelijke winnaar, en dit is vooral duidelijk bij het gebruik van de aggregaattesttechniek. Wat een indrukwekkende prestatie!

Deconstructie en reconstructie van Pauls oplossing

Het deconstrueren en vervolgens reconstrueren van de oplossing van Paul is een geweldige oefening, en je leert veel terwijl je dit doet. Zoals eerder gesuggereerd, raad ik u aan het proces zelf te doorlopen voordat u verder leest.

De eerste keuze die u moet maken, is de techniek die u zou gebruiken om het gewenste potentiële aantal rijen van 4B te genereren. Paul koos ervoor om een ​​columnstore-tabel te gebruiken en deze te vullen met net zoveel rijen als de vierkantswortel van het vereiste getal, dus 65.536 rijen, zodat je met een enkele kruiskoppeling het vereiste aantal zou krijgen. Misschien denkt u dat u met minder dan 102.400 rijen geen gecomprimeerde rijgroep zou krijgen, maar dit is van toepassing wanneer u de tabel vult met een INSERT-instructie zoals we deden met de tabel dbo.NullBits102400. Het is niet van toepassing wanneer u een columnstore-index maakt op een vooraf ingevulde tabel. Dus Paul gebruikte een SELECT INTO-instructie om de tabel te maken en te vullen als een op rowstore gebaseerde heap met 65.536 rijen, en creëerde vervolgens een geclusterde columnstore-index, wat resulteerde in een gecomprimeerde rijgroep.

De volgende uitdaging is uitzoeken hoe je een cross-join kunt laten verwerken met een batch-modusoperator. Hiervoor moet het join-algoritme hash zijn. Onthoud dat een kruisverbinding wordt geoptimaliseerd met behulp van het algoritme voor geneste lussen. Je moet de optimizer op de een of andere manier misleiden om te denken dat je een innerlijke equijoin gebruikt (hash vereist ten minste één op gelijkheid gebaseerd predikaat), maar zorg in de praktijk voor een cross-join.

Een voor de hand liggende eerste poging is om een ​​inner join te gebruiken met een artificieel join-predikaat dat altijd waar is, zoals:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON 0 = 0;

Maar deze code mislukt met de volgende fout:

De optimizer van SQL Server herkent dat dit een kunstmatig inner join-predikaat is, vereenvoudigt de inner join tot een cross-join en produceert een fout die zegt dat het niet kan voldoen aan de hint om een ​​hash-join-algoritme te forceren.

Om dit op te lossen, creëerde Paul een INT NOT NULL-kolom (meer over waarom deze specificatie binnenkort wordt genoemd) met de naam n1 in zijn dbo.CS-tabel, en vulde deze met 0 in alle rijen. Vervolgens gebruikte hij het join-predikaat N2.n1 =N1.n1, waarmee hij effectief de propositie 0 =0 kreeg in alle wedstrijdevaluaties, terwijl hij voldeed aan de minimale vereisten voor een hash-joinalgoritme.

Dit werkt en levert een all-batch-mode plan op:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON N2.n1 = N1.n1;

Wat betreft de reden waarom n1 moet worden gedefinieerd als INT NOT NULL; waarom NULL's niet toestaan ​​en waarom BIGINT niet gebruiken? De reden voor deze keuzes is om een ​​hash-probe-residu te vermijden (een extra filter dat door de hash-join-operator wordt toegepast naast het oorspronkelijke join-predikaat), wat zou kunnen leiden tot extra onnodige kosten. Zie het artikel van Paul Deelnemen aan prestaties, impliciete conversies en restanten voor meer informatie. Dit is het deel uit het artikel dat voor ons relevant is:

Houd er rekening mee dat deze optimalisatie niet van toepassing is op bigint-kolommen."

Laten we om dit aspect te controleren een andere tabel maken met de naam dbo.CS2 met een nullable n1-kolom:

DROP TABLE IF EXISTS dbo.CS2;
 
SELECT * INTO dbo.CS2 FROM dbo.CS;
 
ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL;
 
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS2
WITH (MAXDOP = 1);

Laten we eerst een query testen tegen dbo.CS (waar n1 is gedefinieerd als INT NOT NULL), 4B basisrijnummers genereren in een kolom met de naam rn, en het MAX-aggregaat toepassen op de kolom:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    JOIN dbo.CS AS N2
        ON N2.n1 = N1.n1
) AS N;

We zullen het plan voor deze query vergelijken met het plan voor een vergelijkbare query tegen dbo.CS2 (waarbij n1 is gedefinieerd als INT NULL):

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS2 AS N1
    JOIN dbo.CS2 AS N2
        ON N2.n1 = N1.n1
) AS N;

De plannen voor beide zoekopdrachten worden weergegeven in Afbeelding 10.

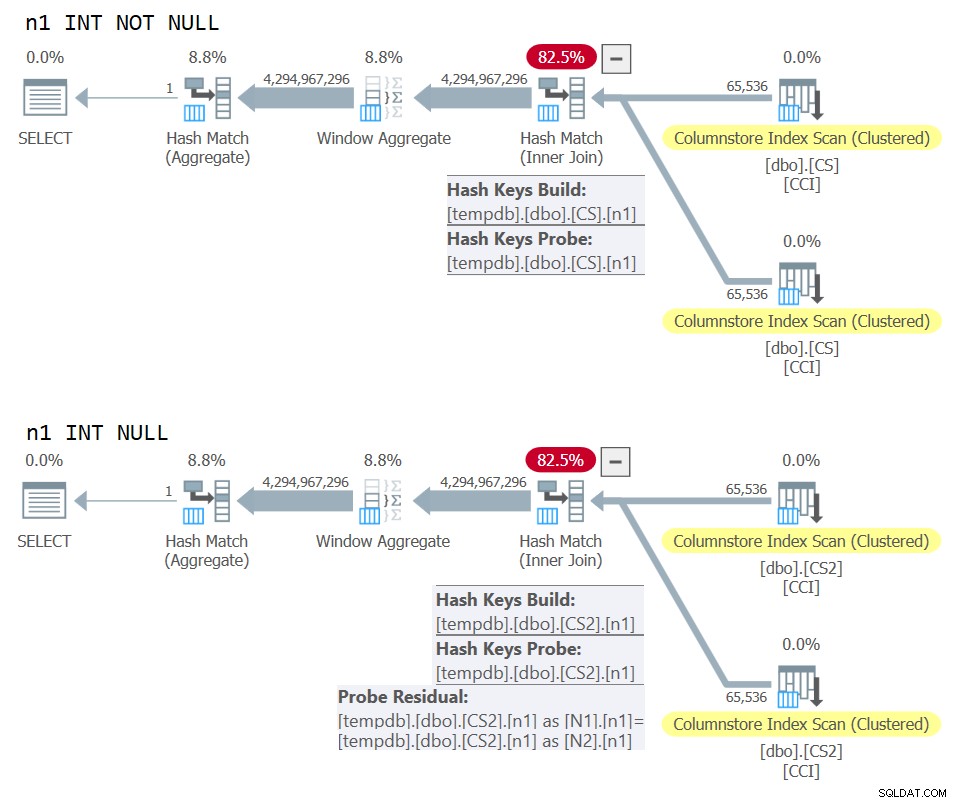Figuur 10:Vergelijking van plannen voor NOT NULL vs NULL join-sleutel

Je kunt duidelijk het extra sonde-residu zien dat in het tweede plan wordt toegepast, maar niet in het eerste.

Op mijn computer werd de query tegen dbo.CS voltooid in 91 seconden en de query tegen dbo.CS2 voltooid in 92 seconden. In het artikel van Paul meldt hij een verschil van 11% ten gunste van de NOT NULL-zaak voor het voorbeeld dat hij gebruikte.

Trouwens, degenen met een scherp oog zullen het gebruik van ORDER BY @@TRANCOUNT als de bestelspecificatie van de ROW_NUMBER-functie hebben opgemerkt. Als je de inline opmerkingen van Paul in zijn oplossing aandachtig leest, vermeldt hij dat het gebruik van de functie @@TRANCOUNT een parallellisme-remmer is, terwijl het gebruik van @@SPID dat niet is. U kunt dus @@TRANCOUNT gebruiken als runtimeconstante in de bestelspecificatie als u een serieel abonnement wilt forceren en @@SPID als u dat niet wilt.

Zoals vermeld, kostte het de query tegen dbo.CS 91 seconden om op mijn computer te draaien. Op dit punt kan het interessant zijn om dezelfde code te testen met een echte cross-join, waarbij de optimizer een geneste loops-join-algoritme in rijmodus kan gebruiken:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    CROSS JOIN dbo.CS AS N2
) AS N;

Het kostte deze code 104 seconden om op mijn machine te voltooien. We krijgen dus een aanzienlijke prestatieverbetering met de batch-mode hash-join.

Ons volgende probleem is het feit dat wanneer je TOP gebruikt om het gewenste aantal rijen te filteren, je een plan krijgt met een rijmodus Top-operator. Hier is een poging om de functie dbo.GetNums_SQLkiwi te implementeren met een TOP-filter:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT TOP (100000000 - 1 + 1)
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        ORDER BY rn
    ) AS N;
GO

Laten we de functie testen:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ik heb het plan dat in figuur 11 wordt getoond voor deze test.

Figuur 11:Plan met TOP-filter

Merk op dat de Top-operator de enige in het plan is die rijmodusverwerking gebruikt.

Ik heb de volgende tijdstatistieken voor deze uitvoering:

Het grootste deel van de runtime in dit plan wordt besteed door de rijmodus Top-operator en het feit dat het plan de batch-naar-rij-modus-conversie en terug moet doorlopen.

Onze uitdaging is om een ​​batch-mode filteralternatief te bedenken voor de row-mode TOP. Op predikaten gebaseerde filters, zoals filters die worden toegepast met de WHERE-component, kunnen mogelijk worden verwerkt met batchverwerking.

Paul's benadering was om een ​​tweede INT-getypte kolom te introduceren (zie de inline opmerking "alles is sowieso genormaliseerd naar 64-bit in columnstore/batch-modus" ) n2 aangeroepen naar de tabel dbo.CS, en vul deze in met de gehele reeks 1 tot en met 65.536. In de code van de oplossing gebruikte hij twee op predikaten gebaseerde filters. Een daarvan is een grof filter in de inner query met predikaten waarbij de kolom n2 aan beide zijden van de join betrokken is. Dit grove filter kan enkele valse positieven tot gevolg hebben. Hier is de eerste simplistische poging tot zo'n filter:

WHERE
    -- Coarse filter:
    N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

Met de ingangen 1 en 100.000.000 als @low en @high krijg je geen false positives. Maar probeer met 1 en 100.000,001, en je krijgt wat. U krijgt een reeks van 100.020.001 getallen in plaats van 100.000.001.

Om de valse positieven te elimineren, voegde Paul een tweede, nauwkeurig filter toe met de kolom rn in de buitenste zoekopdracht. Hier is de eerste simplistische poging tot zo'n nauwkeurig filter:

WHERE
    -- Precise filter:
    N.rn < @high - @low + 2

Laten we de definitie van de functie herzien om de bovenstaande predikaatgebaseerde filters te gebruiken in plaats van TOP, neem 1:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        N.rn < @high - @low + 2;
GO

Laten we de functie testen:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ik heb het plan dat in figuur 12 wordt getoond voor deze test.

Figuur 12:Plan met WHERE-filter, neem 1

Helaas, er is duidelijk iets misgegaan. SQL Server heeft ons op predikaten gebaseerde filter met de kolom rn geconverteerd naar een op TOP gebaseerde filter en geoptimaliseerd met een Top-operator, en dat is precies wat we probeerden te vermijden. Om nog erger te maken, heeft de optimizer ook besloten om het geneste lussen-algoritme voor de join te gebruiken.

Het kostte deze code 18,8 seconden om op mijn machine te voltooien. Ziet er niet goed uit.

Wat betreft de geneste loops join, dit is iets dat we gemakkelijk kunnen oplossen door een join-hint in de inner query te gebruiken. Om de prestatie-impact te zien, volgt hier een test met een geforceerde hash-joinquery-hint die in de testquery zelf wordt gebruikt:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);

De looptijd wordt teruggebracht tot 13,2 seconden.

We hebben nog steeds het probleem met de conversie van het WHERE-filter tegen rn naar een TOP-filter. Laten we proberen te begrijpen hoe dit is gebeurd. We hebben het volgende filter gebruikt in de buitenste zoekopdracht:

WHERE N.rn < @high - @low + 2

Onthoud dat rn staat voor een niet-gemanipuleerde ROW_NUMBER-gebaseerde expressie. Een filter dat gebaseerd is op zo'n ongemanipuleerde uitdrukking die zich in een bepaald bereik bevindt, wordt vaak geoptimaliseerd met een Top-operator, wat voor ons slecht nieuws is vanwege het gebruik van rijmodusverwerking.

De oplossing van Paul was om een ​​equivalent predikaat te gebruiken, maar dan een die manipulatie toepast op rn, zoals:

WHERE @low - 2 + N.rn < @high

Filtering an expression that adds manipulation to a ROW_NUMBER-based expression inhibits the conversion of the predicate-based filter to a TOP-based one. That’s brilliant!

Let’s revise the function’s definition to use the above WHERE predicate, take 2:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        @low - 2 + N.rn < @high;
GO

Test the function again, without any special hints or anything:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

It naturally gets an all-batch-mode plan with a hash join algorithm and no Top operator, resulting in an execution time of 3.177 seconds. Looking good.

The next step is to check if the solution handles bad inputs well. Let’s try it with a negative delta:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

This execution fails with the following error.

Paul’s solution involved two additions. One is to add the following predicate to the inner query’s WHERE clause:

 @high >= @low

This filter does more than what it seems initially. If you’ve read Paul’s inline comments carefully, you could find this part:

The intriguing part here is the potential to use a constant scan with constants as inputs. I’ll get to this shortly.

The other addition is to apply the IIF function to the input expression to the SQRT function. This is done to avoid negative input when using nonconstants as inputs to our numbers function, and in case the optimizer decides to handle the predicate involving SQRT before the predicate @high>=@low.

Before the IIF addition, for example, the predicate involving N1.n2 looked like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

After adding IIF, it looks like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))

With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:

WHERE
    1 >= 100000000
    AND ...

The whole plan can then be simplified to a single Constant Scan operator. Try it:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

The plan for this execution is shown in Figure 13.

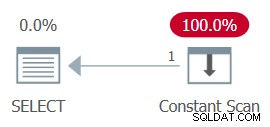Figure 13:Plan with constant scan

Unsurprisingly, I got the following performance numbers for this execution:

logical reads 0

When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.

Now let’s test the function with a valid input range:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

You get the all-batch-mode plan shown in Figure 14.

Figure 14:Plan for dbo.GetNums_SQLkiwi function

This is the same plan you saw earlier in Figure 7.

I got the following time statistics for this execution:

Ladies and gentlemen, I think we have a winner! :)

Conclusie

I’ll have what Paul’s having.

Are we done yet, or is this series going to last forever?

No and no.